Hemmes mathematische Rätsel: Tetrominos
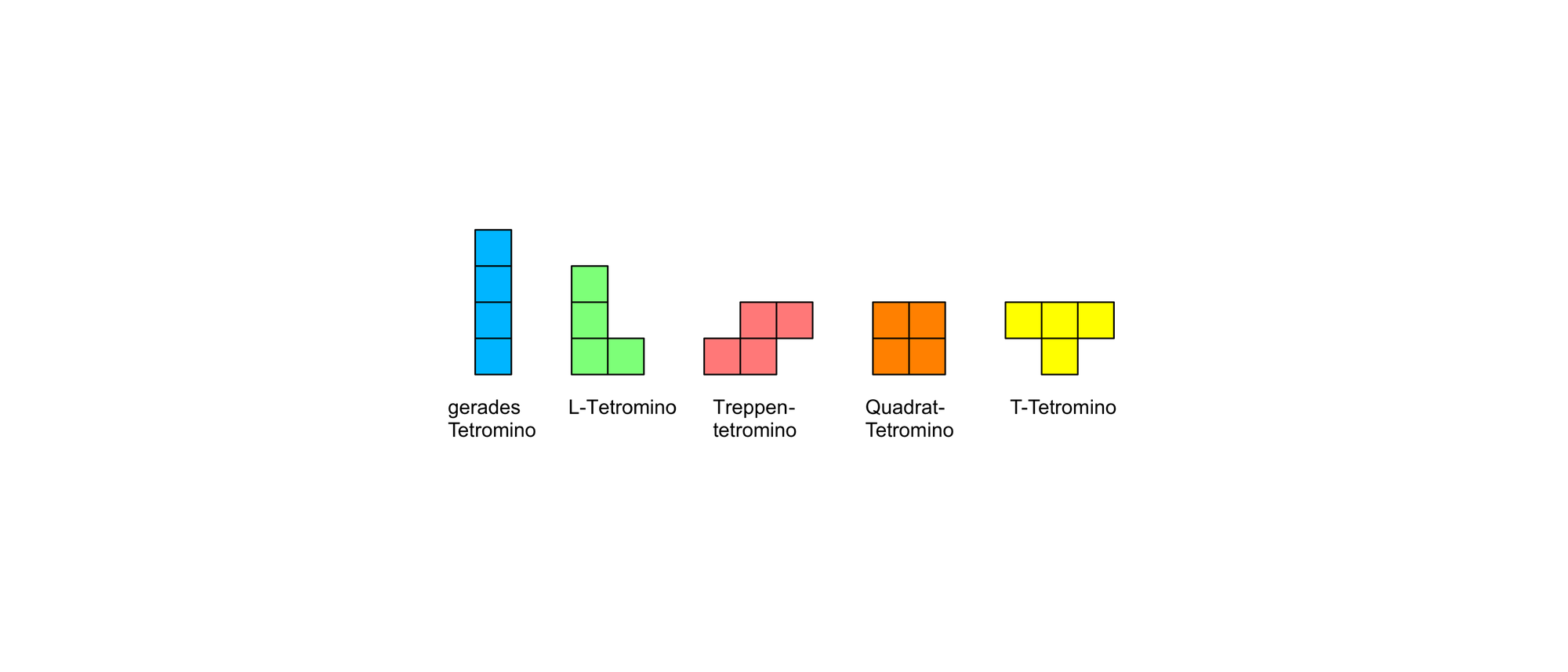
Polyominos sind flache Plättchen, die aus jeweils vier gleichen, an den Kanten zusammenhängenden Quadraten bestehen. Spätestens seit 1907 werden sie für mathematische Knobeleien benutzt und ab den 1930er Jahren in der Zeitschrift »Fairy Chess Review« systematisch untersucht. Der Name »Polyomino« ist jedoch deutlich jünger. Er wurde erst 1953 von dem US-amerikanischen Mathematiker Solomon W. Golomb geprägt. Je nach der Anzahl der Quadrate, aus denen ein einzelnes Polyomino besteht, unterscheidet man Monominos, Dominos, Triominos, Tetrominos, Pentominos usw. Die Tetrominos, die aus jeweils vier Quadraten bestehen, gibt es in fünf unterschiedlichen Formen.
Versucht man, die fünf verschiedenen Tetrominos zu einem 7×3-feldigen Rechteck zusammensetzen, bleibt ein Feld frei. An welchen Positionen kann das freie Feld liegen?
Die Tetrominos dürfen auch umgeklappt werden, das heißt, es dürfen auch ihre Spiegelbilder benutzt werden.
Die Felder des Rechtecks lassen sich schachbrettartig schwarz und weiß färben.
Das gerade Tetromino, das L-Tetromino, das Treppentetromino und das quadratische Tetromino decken jeweils zwei schwarze und zwei weiße Felder des Rechtecks ab. Somit bleiben für das T-Tetromino noch drei schwarze und zwei weiße Felder übrig.
Das T-Tetromino deckt entweder drei schwarze Felder und ein weißes Feld oder drei weiße Felder und ein schwarzes Feld ab. Die zweite Möglichkeit scheidet aus, weil es nur noch zwei weiße Felder gibt. Somit decken die fünf Tetrominos neun weiße und elf schwarze Felder ab und lassen ein weißes Feld frei.
Dass jedes der zehn weißen Felder auch tatsächlich frei bleiben kann, sieht man an den vier Beispielen. Durch Drehen und Spiegeln der vier Anordnungen lässt sich das freie Feld auf jedes weiße Feld bringen.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.