Hemmes mathematische Rätsel: Welche Breiten a, b und c haben die drei Grundstücksteile?
Stefan Itze wurde 1959 in Schweinfurt geboren, studierte Medizin in Erlangen und arbeitete eine Zeitlang in Irland. Seit 1990 ist er in seiner Heimatstadt als Arbeitsmediziner tätig. Im Juni 2020 schickte er mir ein Geometrieproblem, das auf eine wahre Geschichte zurückgeht.
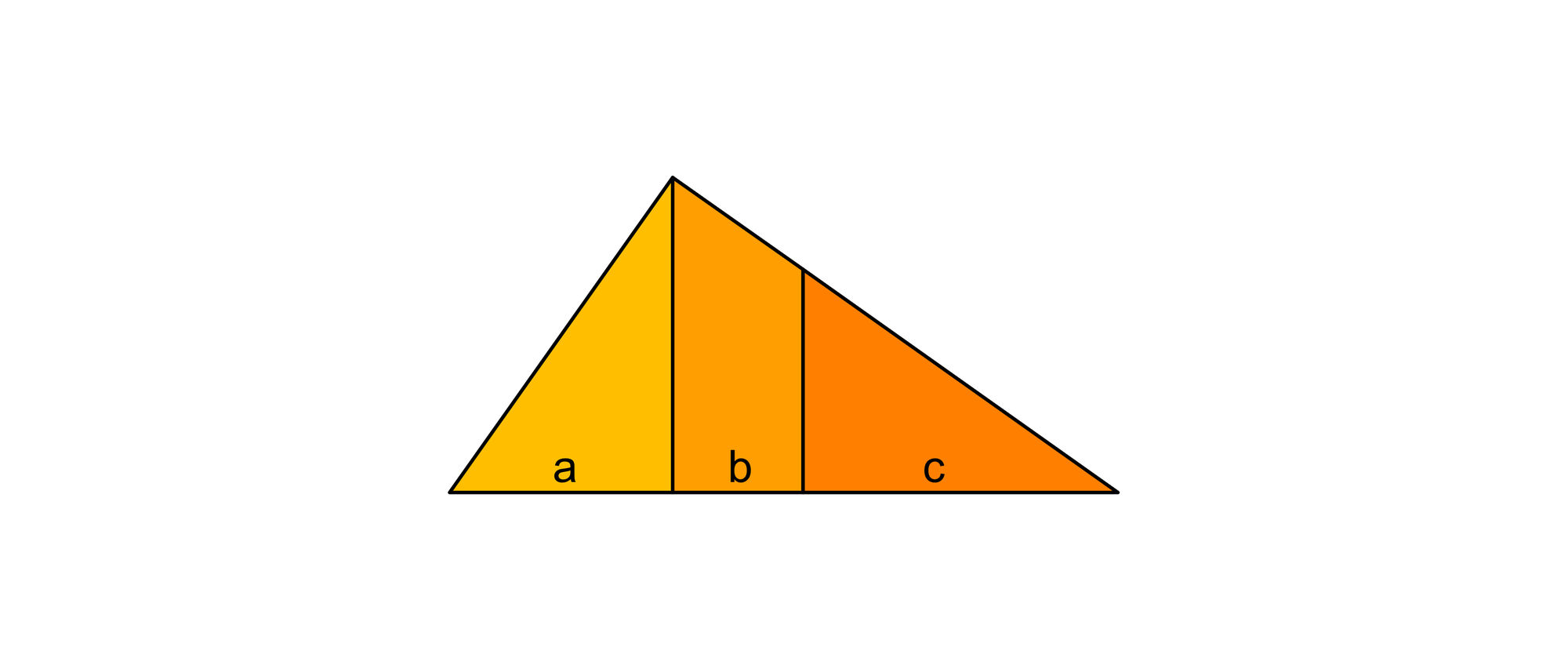
Drei Brüder erbten ein Grundstück am Comer See in Norditalien. Es hatte die Form eines rechtwinkligen Dreiecks. Die Brüder teilten es so, dass jeder ein gleichgroßes Stück bekam. Eine der Teilungslinien war die 100 Meter lange Hypotenusenhöhe des Dreiecks und die zweite eine Parallele dazu. Welche Breiten a, b und c hatten die drei Grundstücksteile?
Das große rote Dreieck hat eine doppelt so große Fläche wie das gelbe. Da es dieselbe Höhe h hat wie das gelbe Dreieck, muss seine Grundseite doppelt so lang sein wie die des gelben Dreiecks. Also ist b + c = 2a. Nach dem Höhensatz des Euklid gilt (b + c)a = h2 oder 2a2 = h2.
Daraus ergibt sich a = 1⁄2√2 · h ≈ 71 m. Das kleine rote Dreieck und das gelbe Dreieck haben die gleiche Fläche und die gleichen Winkel und sind somit deckungsgleich. Also ist c = h = 100 m. Schließlich ist b = 2a − c oder b = (√2 − 1)h ≈ 41 m.
Schreiben Sie uns!
Beitrag schreiben