Hemmes mathematische Rätsel: Welche Fläche nehmen die roten Rechtecke ein?
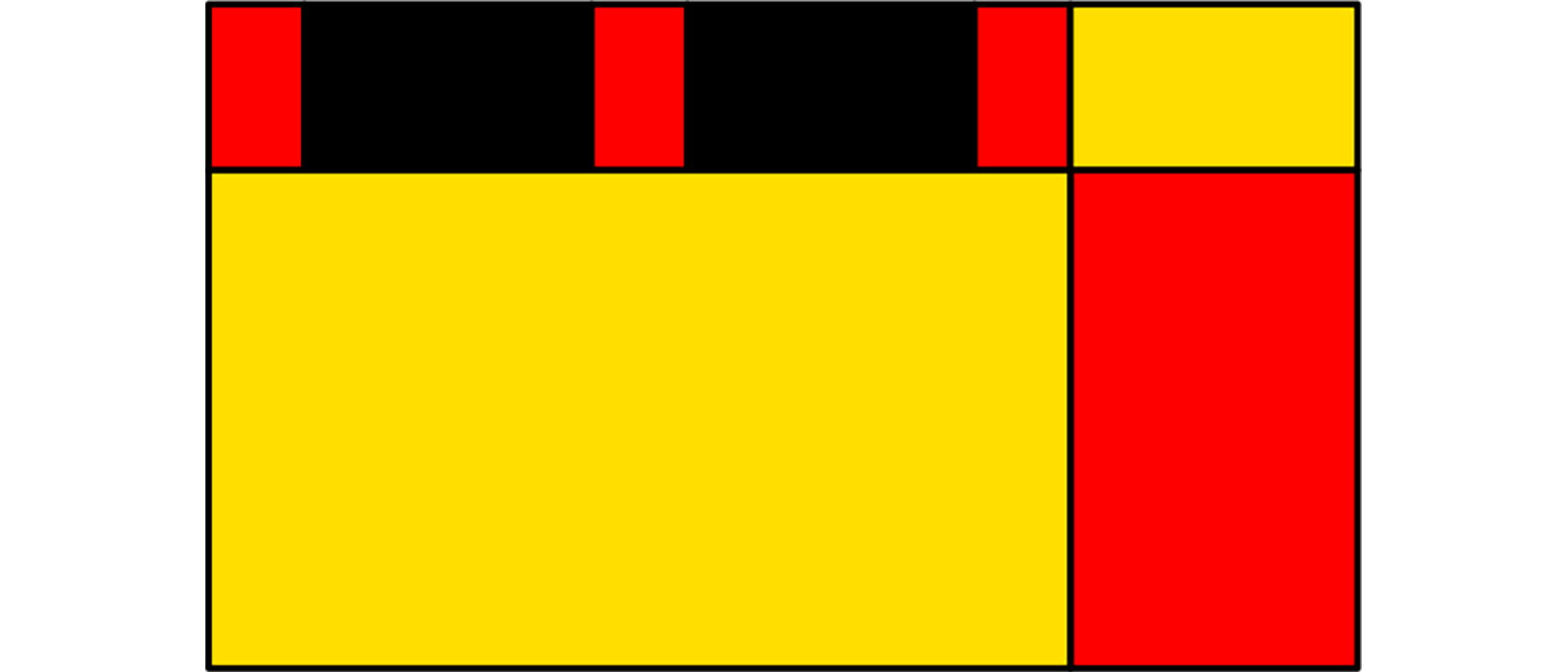
Die beiden gelben, die vier roten und die beiden schwarzen Rechtecke, aus denen sich das Viereck zusammensetzt, sind ähnlich. Den wievielten Teil des Vierecks nehmen die vier roten Rechtecke zusammen ein?
Die beiden schwarzen Rechtecke sind genauso groß wie das kleine gelbe Rechteck. Deshalb färben wir sie auch gelb. Nun fassen wir jedes rote Rechteck mit einem danebenliegenden gelben Rechteck zu einem rot-gelben Rechteck zusammen. Da drei kleine rot-gelbe Rechtecke auf dem großen rot-gelben Rechteck liegen, ist dieses dreimal so lang wie ein kleines rot-gelbes Rechteck. Wegen der Ähnlichkeit der Rechtecke ist es auch dreimal so hoch. Das große rote Rechteck am rechten Rand des Vierecks und das darüberliegende gelbe Rechteck sind gleich breit. Da das rote Rechteck aber dreimal so hoch ist wie das gelbe, ist seine Fläche auch dreimal so groß. Folglich stehen in jedem rot-gelben Rechteck die rote und die gelbe Fläche im Verhältnis 1 : 3. Somit nimmt die gesamte rote Fläche ein Viertel der Vierecksfläche ein.
Hat Ihnen dieses Rätsel gefallen? Dann rätseln Sie doch einfach direkt weiter:
- Welche sechsstelligen Zahlen sind gesucht?
- Wie groß ist die Fläche des Trapezes?
- Wie können die Zahlen noch verteilt werden?
- Warum stimmt diese Aussage?
- Wie lang ist die Sehne des Kreises?
- Welche Zahl fehlt?
- Wie kann das Rätsel gelöst werden?
- Wie viele dieser Zahlen gibt es?
- Wie viel deckt das Quadrat ab?
- Wie muss das Streichholz umgelegt werden?
- Welche Uhrzeit ist gesucht?
- Wie viel Prozent decken die Preise ab?
Eine Übersicht über alle Matherätsel finden Sie unter https://www.spektrum.de/raetsel/. Viel Spaß beim Weiterknobeln!
Schreiben Sie uns!
3 Beiträge anzeigen