Hemmes mathematische Rätsel: Welchen Radius hat der Halbkreis und wie lang ist die mittlere Sehne?
Das heutige Rätsel stammt von Manfred Pietsch aus Kreuzau in Nordrhein-Westfalen und wurde von ihm erstmals 2020 in den »Aachener Nachrichten« und in der »Aachener Zeitung« veröffentlicht.
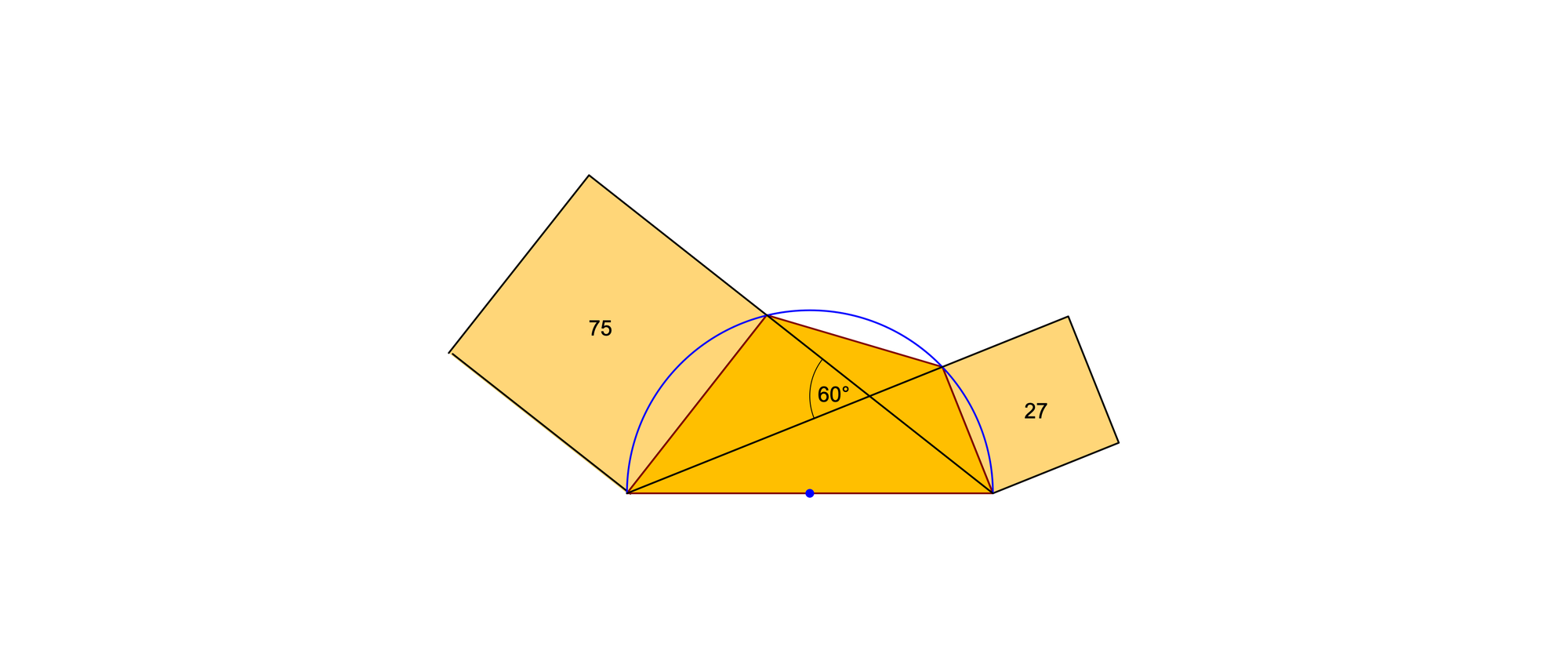
Auf einem Halbkreis liegen zwei Punkte so, dass zusammen mit den Endpunkten des Durchmessers ein Viereck entsteht, dessen Diagonalen sich unter einem Winkel von 60 Grad schneiden. Die Quadrate, die man über die beiden äußeren Sehnen errichten kann, haben Flächeninhalte von 75 und 27. Welchen Radius hat der Halbkreis und wie lang ist die mittlere Sehne?
Nach dem Satz von Thales haben die Dreiecke BDA und BCA an den Ecken D und C rechte Winkel. Dadurch sind die beiden Dreiecke SDA und BCS ebenfalls rechtwinklig. Ihre beiden anderen Winkel sind 60° und 30° groß. Somit sind diese beiden Dreiecke »halbe« gleichseitige Dreiecke, deren kurze Katheten halb so lang sind wie ihre Hypotenusen. Für die Hypotenusenlänge x des Dreiecks SDA gilt nach dem Satz des Pythagoras (√75)2 + (x/2)2 = x2, was sich zu x = 10 umformen lässt. Entsprechend gilt für die kurze Kathete des Dreiecks BCS (√27)2 + y2 = (2y)2, woraus man y = 3 bekommt. Die Diagonale AC des Vierecks ist folglich x + y = 13 lang. Nun kann man mit dem Satz des Pythagoras aus dem Dreieck BCA den Radius des Halbkreises zu r = √(132 + 27)/2 = 7 bestimmen.
Der Winkel DAC = 30° ist ein Umfangswinkel der Sehne CD. Da bei einem Kreis ein Umfangswinkel einer Sehne stets halb so groß ist wie der dazugehörige Mittelpunktswinkel, muss der Winkel DMC = 60° sein. Folglich ist Dreieck DMC gleichseitig und die Sehne CD hat die Länge r = 7.
Schreiben Sie uns!
Beitrag schreiben