Hemmes mathematische Rätsel: Welchen Winkel schließen die Seitenflächen und die Grundfläche ein?
Das heutige Rätsel ist ein dreidimensionales geometrisches Problem und recht vertrackt, wenn man nicht auf den richtigen Kniff kommt.
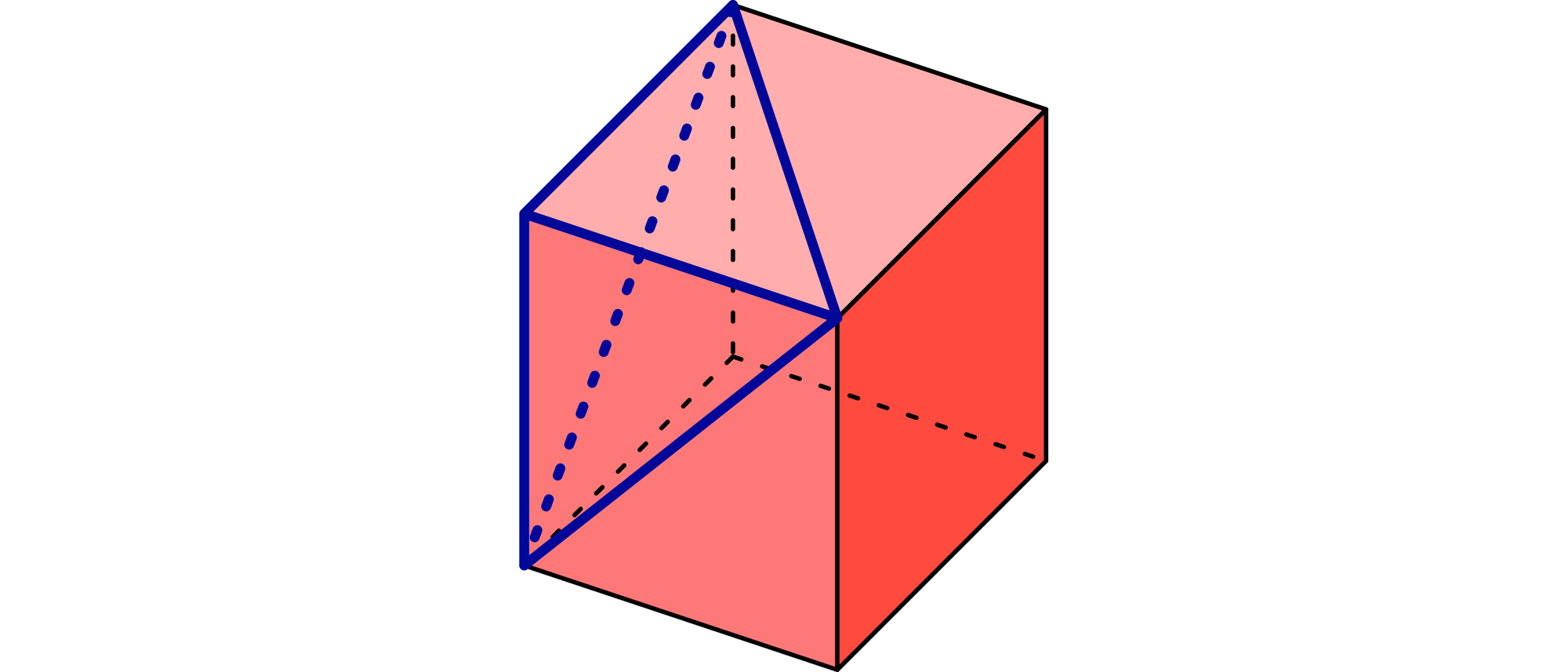
Schneidet man von einem Würfel eine Ecke ab und legt dabei den Schnitt durch die drei benachbarten Ecken, erhält man eine Pyramide mit einem gleichseitigen Dreieck als Grundfläche und drei rechtwinkligen Dreiecken als Seitenflächen. Wie groß ist der Winkel, den die Seitenflächen mit der Grundfläche einschließen?
Hat ein Würfel die Kantenlänge a, so lässt sich mit dem Satz des Pythagoras leicht zeigen, dass für die Länge b seiner halben Flächendiagonalen a2 = 2b2 gilt. Die Würfelkante a, die halbe Flächendiagonale b und die Strecke c bilden das grüne rechtwinkliges Dreieck. Die Strecken b und c schließen dabei den gesuchten Winkel ein, den man nun mit dem Arcus Tangens berechnen kann: arctan(a/b) = arctan((√2)b/b) = arctan(√2) ≈ 54,7°.
Schreiben Sie uns!
Beitrag schreiben