Hemmes mathematische Rätsel: Welches Volumen hat die durchbohrte Kugel?
1932 veröffentlichte der Mathematiker Samuel I. Jones in Nashville in Tennessee sein Buch »Mathematical Nuts«. Es ist eine Sammlung von Knobeleien für Liebhaber der Mathematik und des Denksports. Auf Seite 86 findet man folgende Aufgabe:
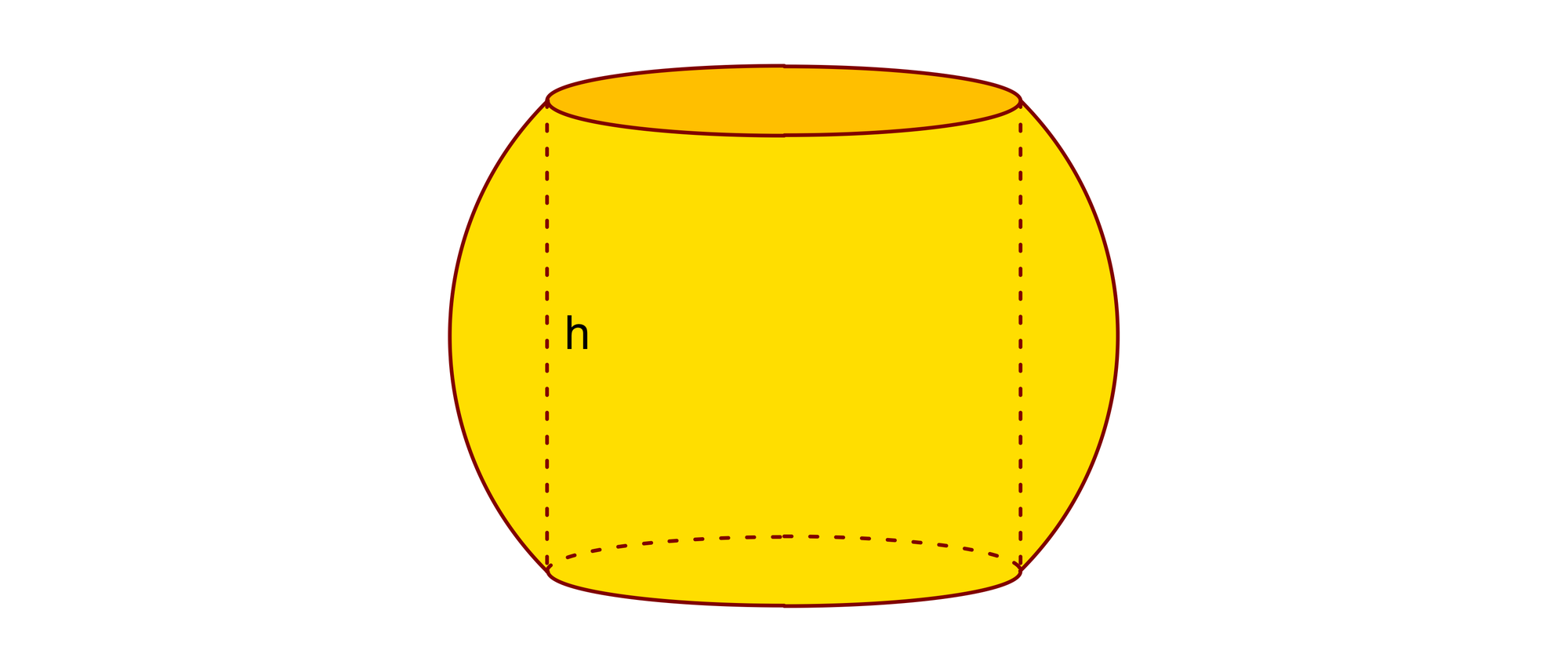
Durch die Mitte einer Kugel wurde ein zylindrisches Loch gebohrt. Die Wandhöhe h der Bohrung beträgt sechs Zentimeter. Wie groß ist das Restvolumen der Kugel, also Kugelvolumen minus Volumen der Bohrung?
Auch wenn es auf den ersten Blick nicht so scheint, lässt sich die Aufgabe ohne weitere Angaben eindeutig lösen.
Bei dem Problem scheint ein Wert zu fehlen, aber das stimmt nicht. Wenn der Durchmesser der Bohrung d ist, dann können wir vom allgemeinen Kugelvolumen das Volumen der zylindrischen Bohrung und das der beiden Kugelkappen abziehen. Dabei fällt dann die Größe d nach etlichen Umformungen wieder aus der Rechnung heraus, und wir erhalten ein eindeutiges Ergebnis. Das Verfahren ist aber sehr umständlich und nicht besonders elegant. Es geht auch viel einfacher.
Der letzte Satz der Aufgabe sagt, dass das Problem ohne weitere Angaben lösbar sei. Das heißt, der Durchmesser des Lochs scheint keine Rolle zu spielen und darf deshalb auch 0 sein. Dann ist das Restvolumen eine massive Kugel mit einem Radius r = 3 cm. Mit der Kugelformel erhält man somit ein Volumen von V = 4/3πr3 = 36π cm3 ≈ 113 cm3.
Jones bringt übrigens in seinem Buch die umständliche Lösung. Die elegante und knappe Lösung stammt von John W. Campbell Jr. und wird erstmals 1959 in Martin Gardners Buch »The Scientific American Book of Mathematical Puzzles and Diversions« veröffentlicht.
Schreiben Sie uns!
Beitrag schreiben