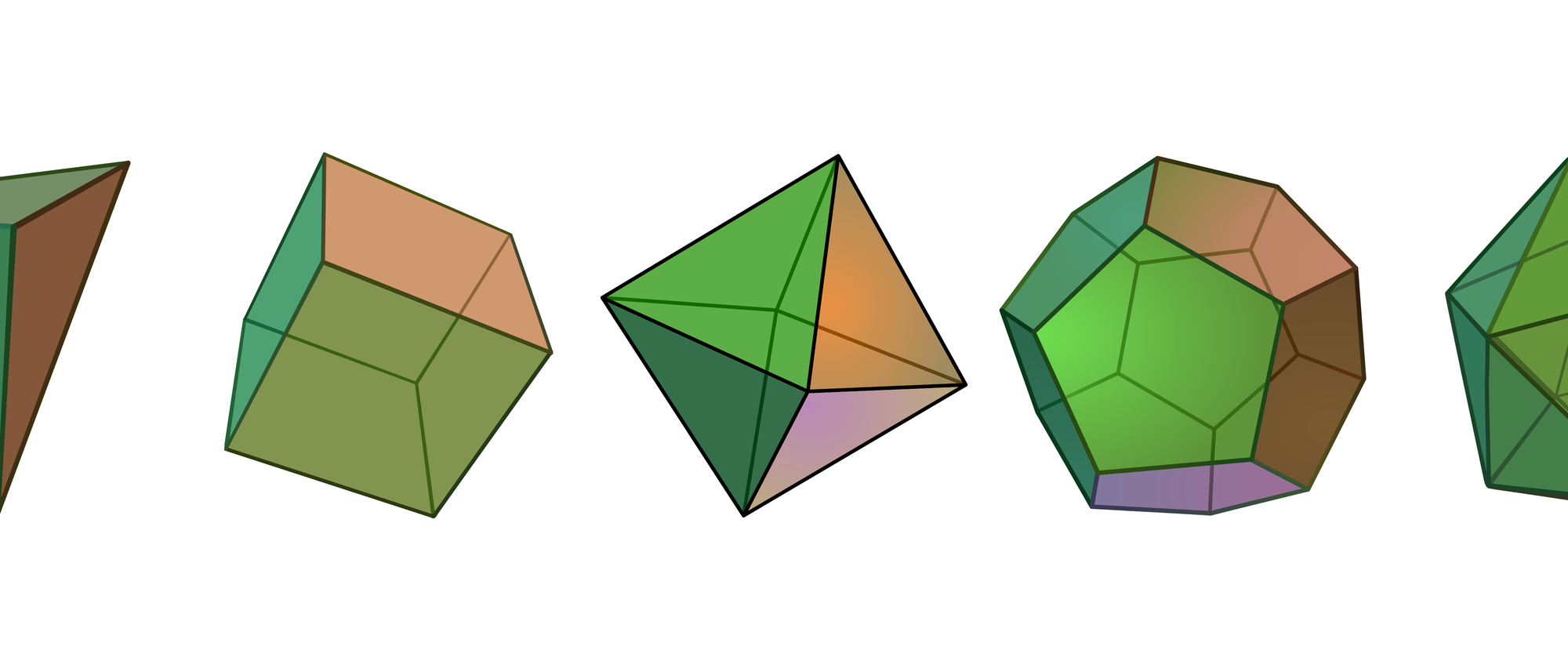
Normalerweise verwendet man als Spielwürfel sechsflächige Kuben mit den Augenzahlen von 1 bis 6. Man kann aber stattdessen auch die vier anderen platonischen Körper – das Tetraeder, das Oktaeder, das Dodekaeder und das Ikosaeder – als Spielwürfel benutzen und tatsächlich auch in jedem Spielzeuggeschäft kaufen. Mit ihnen kann man die Augenzahlen von 1 bis 4, bis 8, bis 12 und bis 20 würfeln.

Beim Oktaeder, Dodekaeder und Ikosaeder zeigt nach dem Wurf, genau wie beim Kubus, eine Fläche nach oben und gibt die erreichte Augenzahl an. Beim Tetraeder ist dies leider unmöglich, denn bei ihm kann nur eine Spitze nach oben zeigen. Um das Tetraeder trotzdem zum Würfeln verwenden zu können, wählen die Hersteller zwei verschiedene, aber gleichwertige Methoden. Die Einen beschriften die vier Ecken mit den Zahlen von 1 bis 4, und die nach dem Wurf nach oben zeigende Ecke gibt das Ergebnis an (oranges Tetraeder).

Die anderen beschriften die Kanten rund um jede Fläche mit den Zahlen von 1 bis 4, und die unsichtbare Fläche, auf die das Tetraeder nach einem Wurf fällt, gibt das Ergebnis an (rosa Tetraeder). In den Zeichnungen ist also in beiden Fällen ein 1 gewürfelt worden.

Es gibt aber noch eine dritte Möglichkeit. Auf den vier Seiten eines Tetraeders stehen vier Zahlen. Würfelt man nun mit diesem Tetraeder, ist das Ergebnis die Summe der Zahlen auf den drei sichtbaren Seiten. Natürlich soll man mit diesem Tetraeder trotzdem genau die Zahlen 1, 2, 3 und 4 werfen können. Welche Zahlen, die weder ganzzahlig noch positiv zu sein brauchen, müssen auf den Flächen stehen?