Hemmes mathematische Rätsel: Wie groß ist der Flächeninhalt des roten Dreiecks?
Das heutige Rätsel ist wieder einmal ein Problem aus der ebenen Geometrie. Es wurde Gerd Ehrhardt aus Aachen erdacht und erstmals 2019 in der »Aachener Zeitung« und in den »Aachener Zeitung« veröffentlicht.
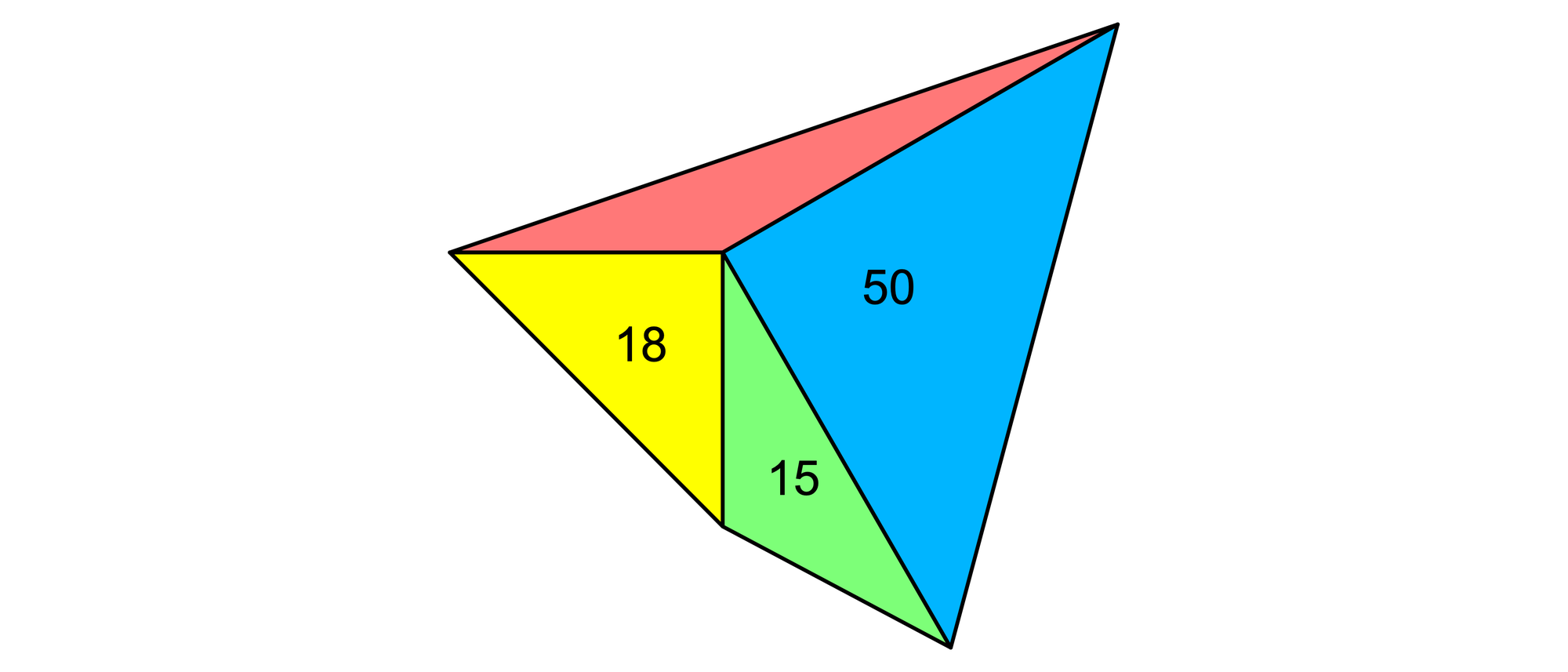
Ein unregelmäßiges Viereck setzt sich aus vier Dreiecken zusammen, die an einem Punkt zusammentreffen. Das gelbe und das blaue Dreieck sind rechtwinklig und gleichschenklig. Der Flächeninhalt des grünen Dreiecks beträgt 15 cm2, der des gelben 18 cm2 und der des blauen 50 cm2. Wie groß ist der Flächeninhalt des roten Dreiecks?
Der Flächeninhalt eines Dreiecks ist das halbe Produkt seiner Grundlinie und seiner Höhe. Dies reicht zur Lösung der Aufgabe aus. Man braucht das grüne Dreieck nur um 90° gegen den Uhrzeigersinn um den gemeinsamen Punkt der vier Dreiecke zu drehen, um zu sehen, dass es die gleiche Grundlinie g und die gleiche Höhe h wie das rote Dreieck hat.
Der gesuchte Flächeninhalt des roten Dreiecks beträgt also ebenfalls 15 cm2. Die Flächeninhalte des gelben und des blauen Dreiecks werden für die Lösung des Problems gar nicht benötigt.
Schreiben Sie uns!
Beitrag schreiben