Hemmes mathematische Rätsel: Wie groß ist das Verhältnis von r zu x?
Das heutige Rätsel hat Harald Burda aus Alsdorf in Nordrhein-Westfalen 2021 entworfen. Bei einem lateinischen Kreuz stehen die beiden Balken rechtwinklig zueinander, und der Längsbalken schneidet den Querbalken mittig. Die beiden Balken brauchen nicht gleich lang zu sein.
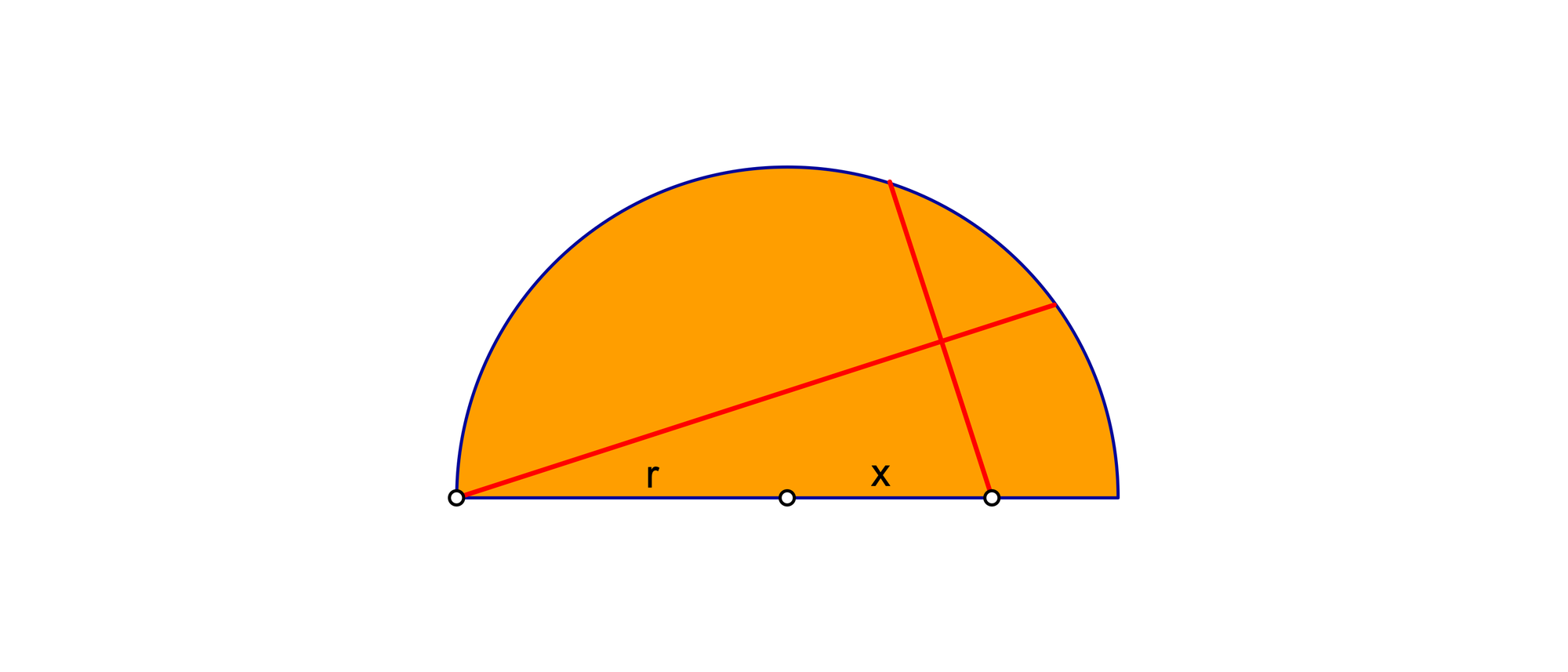
In einem Halbkreis vom Radius r liegt ein lateinisches Kreuz, dessen Querbalken die Länge r hat. Ein Endpunkt des Längsbalkens fällt mit einer Ecke des Halbkreises zusammen, der andere liegt irgendwo auf dem Halbkreisbogen. Auch ein Endpunkt des Querbalkens liegt auf dem Halbkreisbogen. Der zweite Endpunkt liegt auf der Grundseite des Halbkreises in einem Abstand x vom Mittelpunkt des Halbkreises.
Wie groß ist das Verhältnis r/x?
Die beiden rechtwinkligen Dreiecke ABC und ADE sind ähnlich. Darum gilt AC/AB = AE/AD. Mit AC = x/2, AB = r, AE = r/2 und AD = r + x wird daraus x/(2r) = r/(2(r + x)), was sich zu r2 − xr − x2 = 0 umformen lässt.
Diese quadratische Gleichung hat die positive Lösung r = (√5 + 1)x/2. Somit ist das gesuchte Verhältnis r/x = (√5 + 1)/2 ≈ 1,618 der berühmte Goldene Schnitt Φ, ein Streckenverhältnis, das seit der Antike in der Kunst und in der Architektur verwendet und von den Menschen als besonders ästhetisch empfunden wird.
Schreiben Sie uns!
Beitrag schreiben