Hemmes mathematische Rätsel: Wie groß ist das Verhältnis?
Der 1944 geborene Schweizer Mathematiker Hans Walser hat viele Jahrzehnte lang als Lehrer an Gymnasien und als Lehrbeauftragter an Universitäten unterrichtet. Er hat eine große Zahl von Aufsätzen für Fachzeitschriften und auch etwa ein Dutzend Bücher verfasst. Sein neuestes Werk ist im Sommer 2022 erschienen und heißt „Spiralen, Schraubenlinien und spiralartige Figuren“. Im Internet betreibt er eine Seite, die „Miniaturen“ heißt (https://www.walser-h-m.ch/hans/Miniaturen). Von dieser Seite stammt die heutige Kopfnuss.
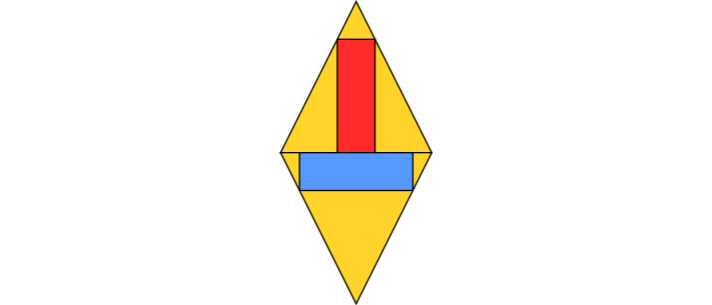
Auf der kurzen Diagonalen eines Rhombus steht hochkant ein rotes Rechteck, das aber kein Quadrat ist, und ein genau gleiches blaues Rechteck hängt quer an dieser Diagonalen. Die beiden oberen Ecken des roten und die beiden unteren Ecken des blauen Rechtecks liegen auf den Rhombusseiten. Wie groß kann das Verhältnis der langen zur kurzen Diagonalen des Rhombus höchstens sein?
Hängt man das quer liegende Rechteck nicht an die kurze Diagonale des Rhombus, sondern setzt es darauf, entsteht das grüne rechtwinklige Dreieck. Haben die langen Seiten der beiden Rechtecke die Länge a und die kurzen die Länge b, so hat die vertikale Kathete des grünen Dreiecks die Länge a – b und die horizontale die Länge 1/2(a – b). Das grüne und das violette Dreieck sind ähnlich. Da die Katheten des violetten Dreiecks halbe Diagonalen des Rhombus sind, beträgt dessen Diagonalenverhältnis folglich (a – b) / (1/2(a – b)) = 2. Das Diagonalenverhältnis des Rhombus ist also immer 2, unabhängig von den Abmessungen des Rechtecks.
Schreiben Sie uns!
Beitrag schreiben