Hemmes mathematische Rätsel: Welches Volumen hat der eckenlose Holzklotz?
2020 dachte sich Manfred Pietsch aus Kreuzau in Nordrhein-Westfalen ein kleines geometrisches Problem aus, das im selben Jahr in der »Aachener Zeitung« und in den »Aachener Nachrichten« erstmals veröffentlicht wurde.
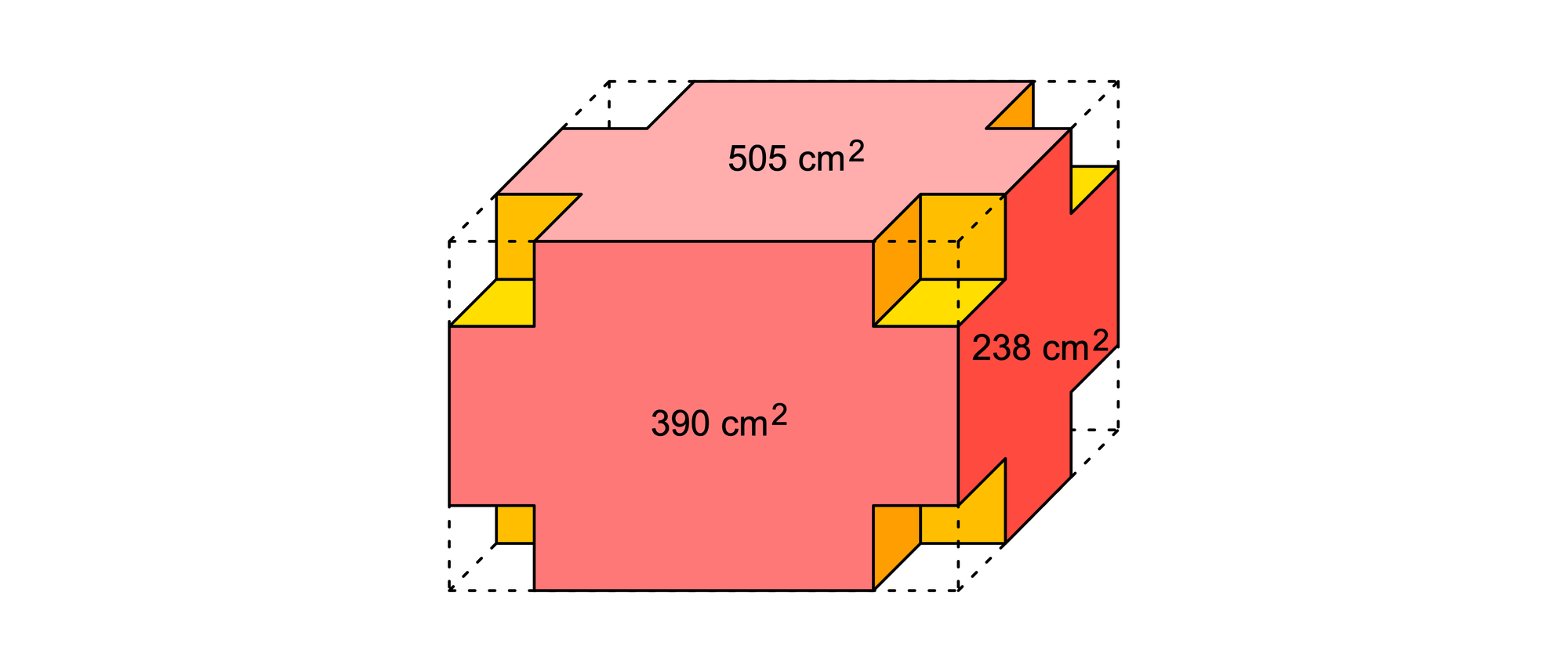
Von einem rotlackierten hölzernen Quader werden an allen acht Ecken Würfel mit einer Kantenlänge von 5 cm ausgefräst. Die verbleibenden kreuzförmigen roten Flächen des Klotzes sind vorne und hinten je 390 cm2 groß, oben und unten je 505 cm2 und links und rechts je 238 cm2 groß. Welches Volumen hat der eckenlose Holzklotz?
Sind a, b und c die Länge, Breite und Höhe des ursprünglichen Quaders, hatte seine Oberseite den Flächeninhalt F1 = ab = 505 cm2 + 4 · 25 cm2 = 605 cm2. Sie war also um 100 cm2 größer als die obere Fläche des eckenlosen Klotzes.
Analog erhält man für die ursprüngliche Vorderfläche F2 = ac = 490 cm2 und für eine ursprüngliche Seitenfläche F3 = bc = 338 cm2. Nun ist F1F2F3 = ab · ac · bc = (abc)2. Zieht man daraus die Wurzel, erhält man das Volumen V = abc = √(F1F2F3) des ursprünglichen Quaders.
Somit gilt V = √(605 · 490 · 338) cm3 = 10010 cm3. Da acht Würfel zu je 125 cm3 ausgefräst wurden, bleibt für den eckenlosen Klotz ein Volumen von 9010 cm3 übrig.
Schreiben Sie uns!
Beitrag schreiben