Hemmes mathematische Rätsel: Wie groß ist der gesamte Flächeninhalt?
© Heinrich Hemme (Ausschnitt)
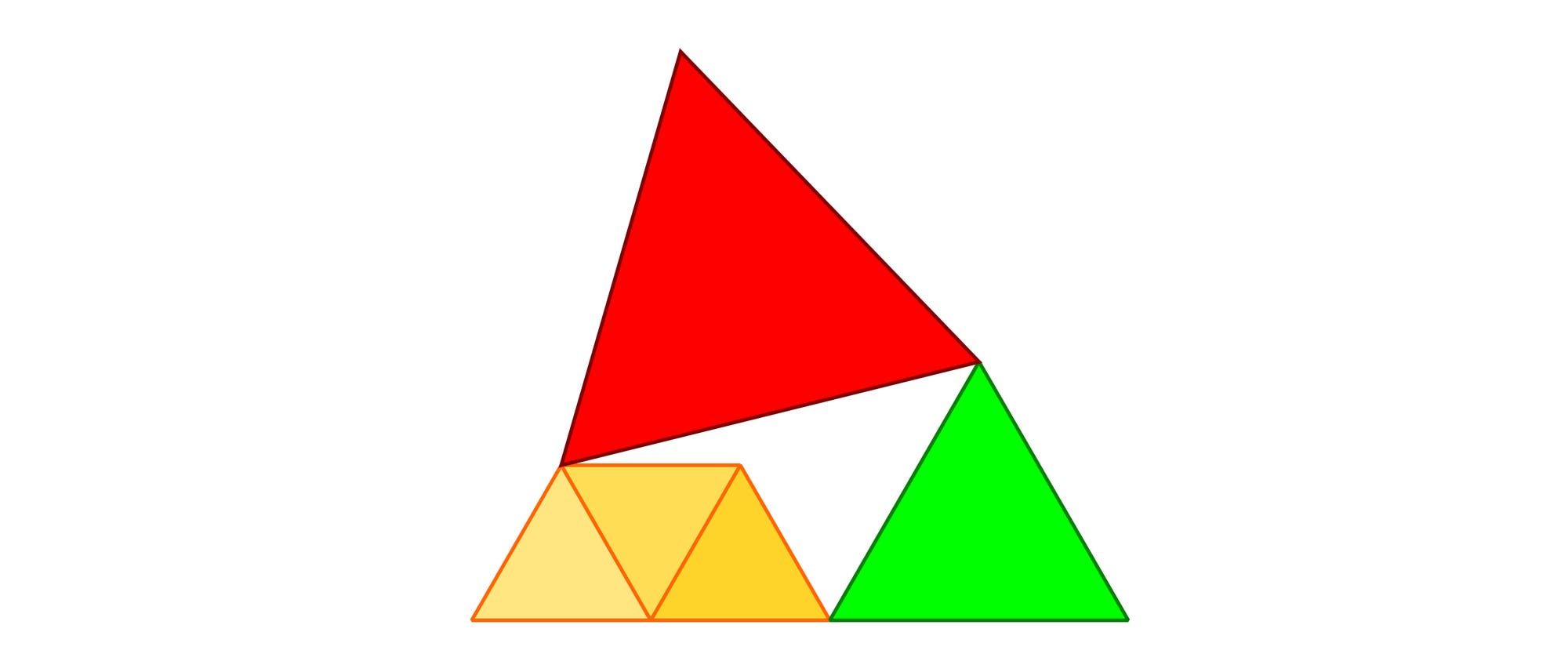
Das rote gleichseitige Dreieck hat den Flächeninhalt 1. Wie groß ist der Gesamtflächeninhalt der vier anderen gleichseitigen Dreiecke?
Die drei gelben Dreiecke lassen sich zu einem regelmäßigen Sechseck verdoppeln. Das darin liegende Dreieck BCD ist gleichseitig und hat den gleichen Flächeninhalt wie die drei gelben Dreiecke zusammen. Der Winkel FDB beträgt 90°, und darum ist das Dreieck BDF rechtwinklig. Folglich gilt nach dem Satz des Pythagoras BD2 + DF2 = BF2. Das bedeutet auch, dass die beiden Dreiecke BCD und DEF zusammen den gleichen Flächeninhalt haben wie das Dreieck ABF. Somit beträgt der Gesamtflächeninhalt der vier kleinen Dreiecke 1.
© Heinrich Hemme (Ausschnitt)
Schreiben Sie uns!
Beitrag schreiben