Hemmes mathematische Rätsel: Wie groß ist der Quotient?
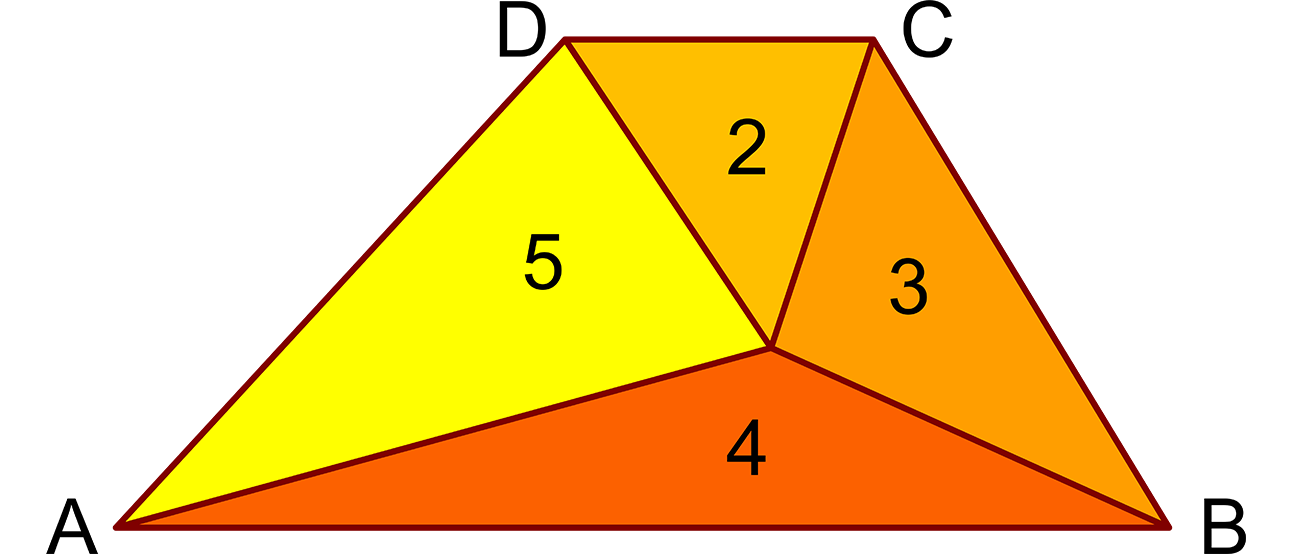
Ein Trapez setzt sich, so wie es das Bild zeigt, aus vier Dreiecken mit den Inhalten 2, 3, 4 und 5 zusammen. Wie groß ist der Quotient AB/CD aus den Längen der beiden parallelen Trapezseiten?
Die Höhen der beiden Dreiecke ABP und CDP auf den Seiten AB und CD sind x und y. Mit den Flächeninhalten 4 und 2 dieser Dreiecke erhält man 1/2 ∙ AB ∙ x = 4 und 1/2 ∙ ACD ∙ y = 2, was man zu x = 8/AB und y = 4/CD umformen kann. Das gesamte Trapez hat den Flächeninhalt 1/2(AB + CD)(x + y) = 2 + 3 + 4 + 5, woraus sich (AB + CD)(x + y) = 28 ergibt. Mit den Ausdrücken für x und y wird daraus (AB + CD)(8/AB + 4/CD) = 28. Dies kann man zu AB/CD + 2 ∙ CD/AB = 4 vereinfachen. Bezeichnet man den Term AB/CD mit z, wird daraus z + 2/z = 4 oder z2 – 4z + 2 = 0. Diese quadratische Gleichung hat die beiden Lösungen z = 2 ± √2. Da AB länger ist als CD, kann AB/CD nur 2 + √2 ≈ 3,41 sein.
Schreiben Sie uns!
2 Beiträge anzeigen