Hemmes mathematische Rätsel: Wie groß ist der Radius des Kreises?
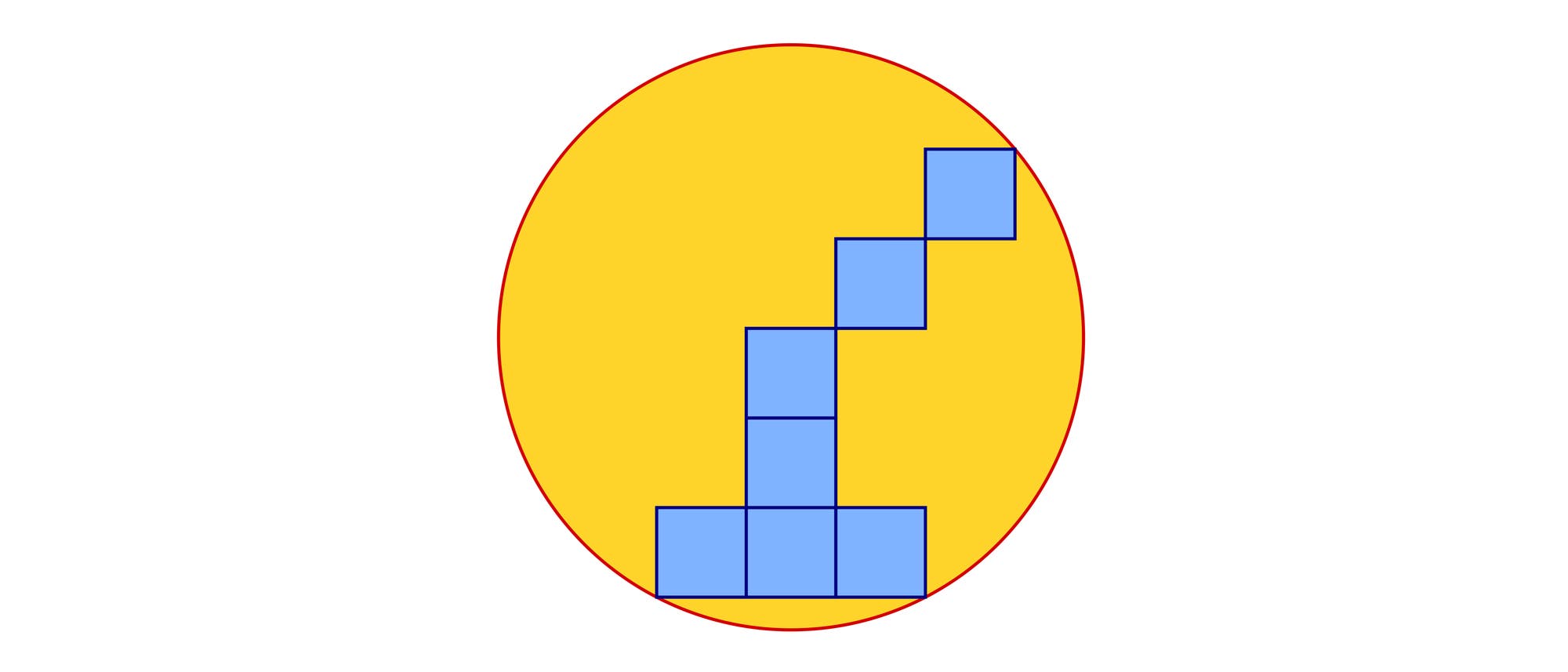
Die folgende Aufgabe stammt von Bernd Bultmann aus Butjadingen. In einem Kreis liegen sieben Quadrate mit der Seitenlänge 10. Drei ihrer Ecken berühren den Kreisumfang. Alle Seiten der Quadrate liegen parallel oder senkrecht zueinander. Wie groß ist der Radius des Kreises?
Der Mittelpunkt M des Kreises mit dem Radius r muss auf der Mittelsenkrechten der Sehne CE liegen. Hat die Strecke MD die Länge x, so gilt nach dem Satz des Pythagoras für das Dreieck CDM die Gleichung r2 = 152 + x2 und für das Dreieck MBA die Gleichung r2 = 252 + (50 – x)2. Die beiden Gleichungen werden gleichgesetzt und man erhält 152 + x2 = 252 + (50 – x)2, was man zu x = 29 vereinfachen kann. Setzt man dies in die erste Gleichung ein, bekommt man r2 = 152 + 292 oder r = √1066 ≈ 32,65.
Schreiben Sie uns!
Beitrag schreiben