Hemmes mathematische Rätsel: Wie groß ist der Umfang des Blütenblattes?
Presh Talwalkar hat Mathematik und Wirtschaftswissenschaften an der Stanford University in Kalifornien in den USA studiert. Er hat einige Bücher über mathematische Knobeleien geschrieben, darunter das im Jahr 2015 erschienene dreibändige Werk »Math Puzzles«. Talwalkar betreibt auch im Internet den Denksport-Blog »Mind Your Decision«. Am 16. August 2022 stellte er seinen Leserinnen und Lesern auf seiner Seite ein kniffliges geometrisches Problem, das er von Chan Lye Lee erhalten hatte, einem Mathematiklehrer, der von der Insel Penang in Malaysia stammt und in Singapur lebt. Lee stellt seit etlichen Jahren auf seinem YouTube-Kanal seinen Zuschauern wöchentlich eine mathematische Knobelaufgabe.
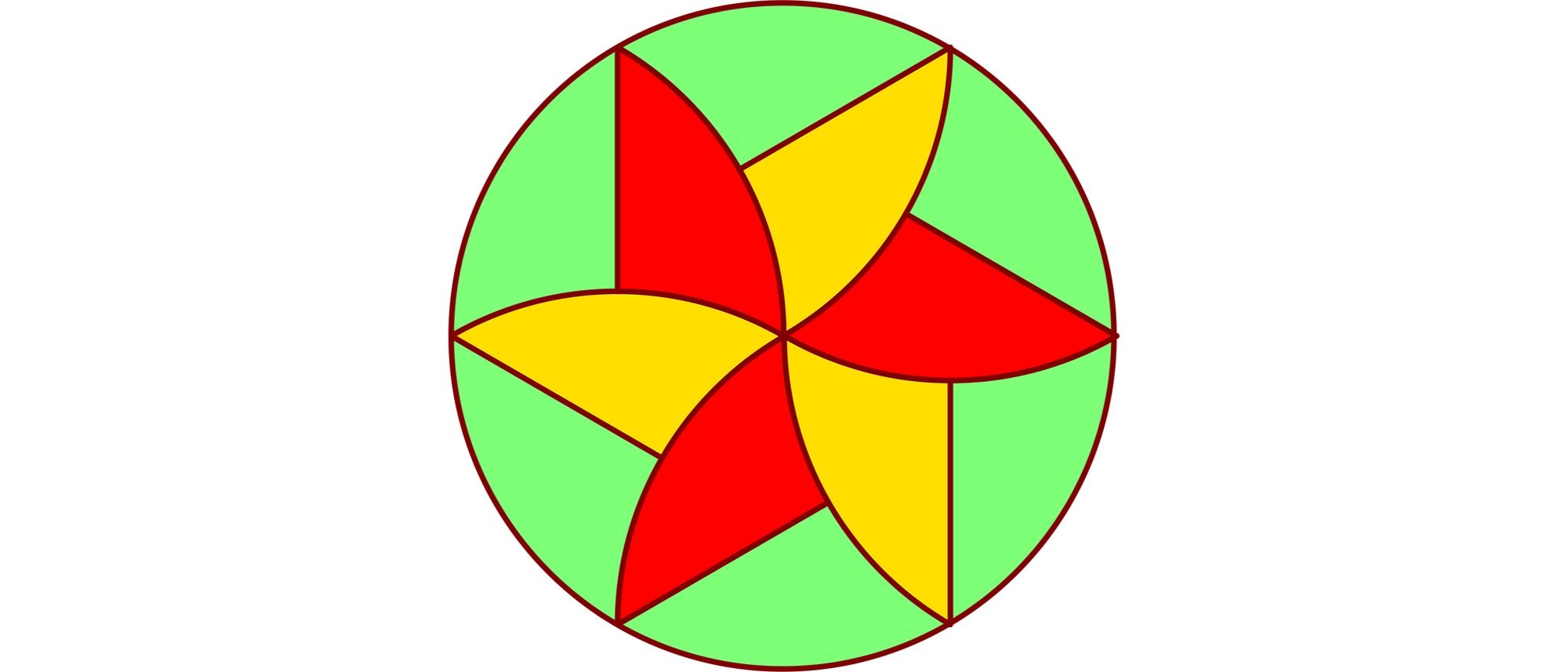
Die sechs roten und gelben Blütenblätter und die sechs grünen Kelchblätter dieser Blumenblüte sind deckungsgleich. Wie groß ist der Umfang eines Blütenblattes, wenn der Radius des Blütenkreises 1 beträgt?
Der Blütenkreis und alle Kreisbögen der Blätter haben den Radius 1. Die Spitzen der Blütenblätter liegen auf den Ecken eines regelmäßigen Sechsecks. Sein Umkreis ist der Blütenkreis, der den Umfang 2π · 1 = 2π hat. Die drei Diagonalen des Sechsecks unterteilen es in sechs gleichseitige Dreiecke der Seitenlänge 1. Der Umfang jedes Blattes setzt sich aus einer Strecke der Länge a, aus einem Sechstelkreisbogen der Länge 2π/6 = π/3 und einem Zwölftelkreisbogen der Länge 2π/12 = π/6 zusammen. Die Höhe eines gleichseitigen Dreiecks der Seitenlänge 1 ist 1/2√3 lang. Folglich hat die Strecke AC die Länge √3 und damit die Strecke AB die Länge a = √3 – 1. Jedes Blatt der Blüte hat somit einen Umfang von π/3 + π/6 + √3 – 1 = π/2 + √3 – 1 ≈ 2,303.
Schreiben Sie uns!
Beitrag schreiben