Hemmes mathematische Rätsel: Wie groß ist die gelbe Fläche?
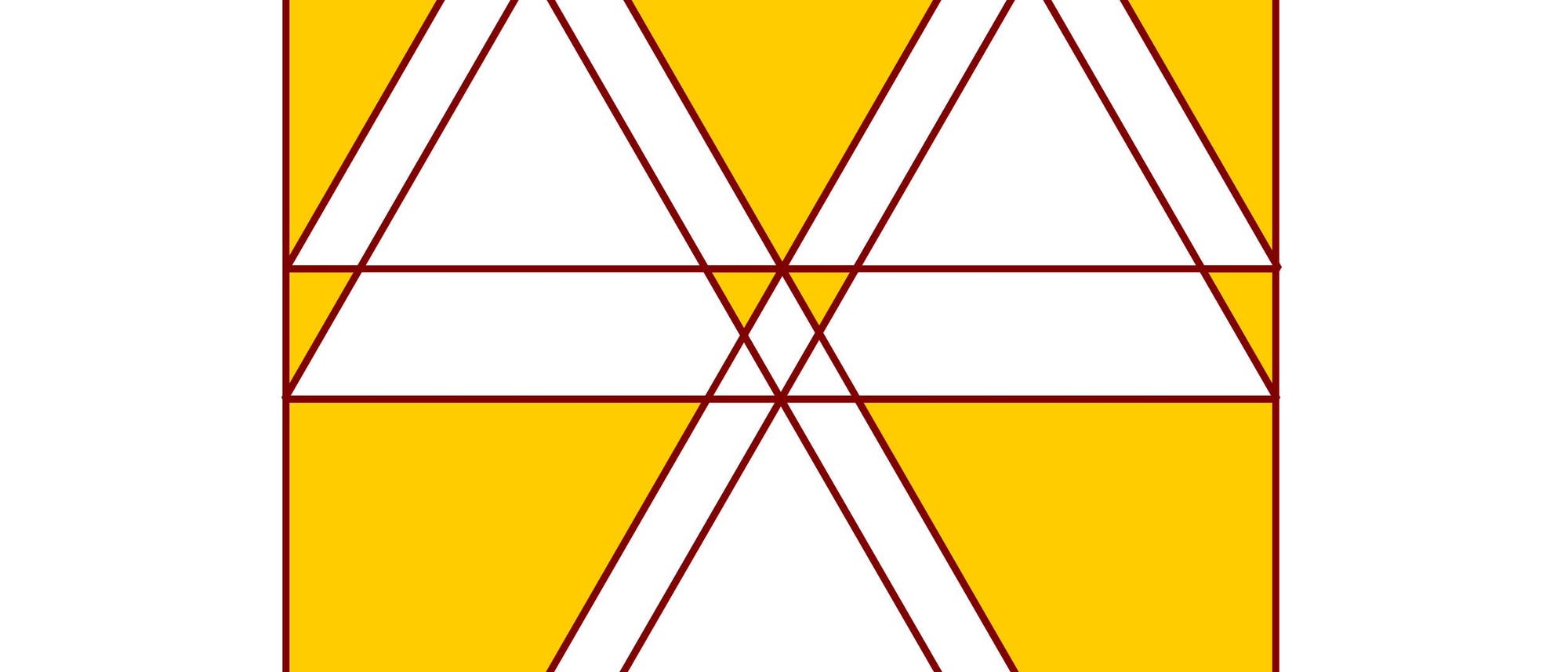
In einem Quadrat der Seitenlänge 8 liegen sechs gleiche gleichseitige Dreiecke so, wie es das Bild zeigt. Wie groß ist die gesamte gelbe Fläche?
In dem Quadrat liegen sechs große weiße Dreiecke mit der Seitenlänge 4 und der Höhe h = 1/2√3 · 4 = 2√3 und der Fläche A = 1/2 · 4 · h = 1/2 · 4 · 2√3 = 4√3. Die großen Dreiecke bilden zwei Dreiergruppen, die um die Strecke a gegeneinander verschoben sind. Dabei hat a den Wert a = 8 – 2h = 8 – 2 · 2√3 = 8 – 4√3. Jedes der beiden kleinen weißen Dreiecke hat die Höhe l = a/2 = (8 – 4√3)/2 = 4 – 2√3 und die Fläche C. Für das Flächenverhältnis der kleinen und großen Dreiecke gilt C/A = (l/h)2 = ((4 – 2√3)/(2√3))2, woraus sich C = ((2 – √3)/√3)2A ergibt. Jedes der drei mittelgroßen weißen Dreiecke hat die Höhe k = h – a = 2√3 – (8 – 4√3) = 6√3 – 8 und die Fläche B. Für das Flächenverhältnis der mittelgroßen und großen Dreiecke gilt B/A = (k/h)2 = ((6√3 – 8)/(2√3))2, woraus sich B = ((3√3 – 4)/√3)2A ergibt. Die gelbe Fläche hat somit die Größe G = 82 – 6A + 3B + 2C = 64 – 6A + 3((3√3 – 4)/√3)2A + 2((2 – √3)/√3)2A = 64 – (6 – 3((3√3 – 4)/√3)2 – 2((2 – √3)/√3)2) · 4√3 = 500/√3 – 256 ≈ 32,675.
Schreiben Sie uns!
Beitrag schreiben