Hemmes mathematische Rätsel: Wie groß ist Gesamtfläche der beiden Halbkreise?
Catriona Agg ist eine britische Lehrerin, die an einer Schule im Norden von Essex Mathematik unterrichtet. Seit Mitte 2018 stellt sie alle paar Tage auf Twitter ihren Leserinnen und Lesern ein mathematisches Rätsel. Am 21. August 2020 twitterte sie folgende Aufgabe:
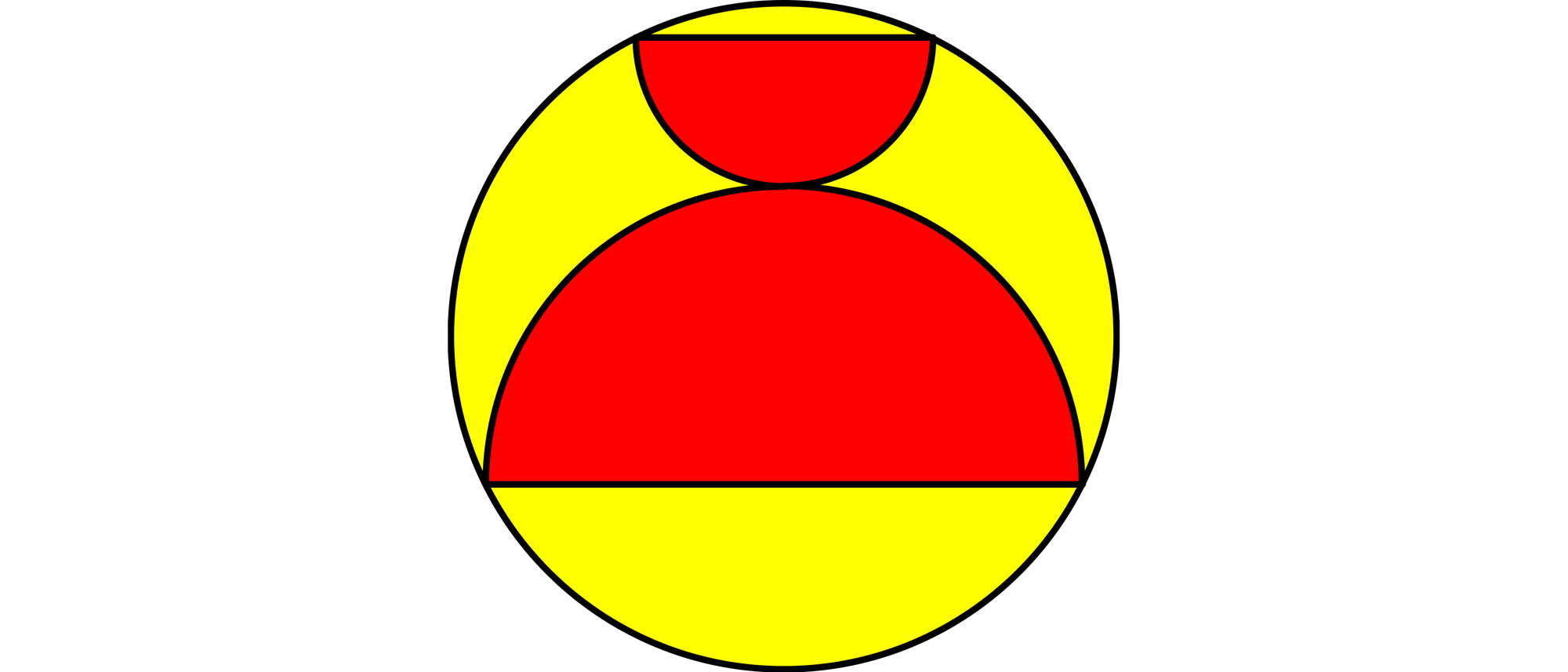
Zwei Halbkreise mit parallelen Grundseiten liegen so in einem Vollkreis, dass ihre Ecken auf dessen Umfang fallen. Der Radius des Vollkreises beträgt 1. Wie groß ist Gesamtfläche der beiden Halbkreise?
Ist das Problem ohne zusätzliche Informationen überhaupt lösbar?
Die Radien vom kleinen Halbkreis, vom großen Halbkreis und vom Vollkreis sind a, b und r, und die Strecke AD verläuft parallel zur Verbindungstecke der Mittelpunkte der Halbkreise und des Vollkreises. Die beiden Winkel ADB und AEF = AEB sind Umfangswinkel über dem Bogen AB und deshalb gleich groß. Folglich sind die beiden rechtwinkligen Dreiecke EAF und DFB ähnlich.
Die Katheten des Dreiecks DFB haben beide die Länge a + b. Folglich sind auch die Katheten des Dreiecks EAF gleich lang. Somit ist x = b − a und damit DA = 2b.
Auf das Dreieck CDA kann man den Satz des Pythagoras anwenden, und man erhält (2a)2 + (2b)2 = (2r)2 oder a2 + b2 = r2. Die Fläche des Kreises beträgt πr2 und die der beiden Halbkreise zusammen πa2/2 + πb2/2 = π(a2 + b2)/2 = πr2/2.
Die beiden Halbkreise nehmen also, unabhängig von ihren Radien, zusammen immer die halbe Kreisfläche ein.
Schreiben Sie uns!
7 Beiträge anzeigen