Hemmes mathematische Rätsel: Wie groß ist die Summe der Flächeninhalte?
Catriona Agg ist eine britische Lehrerin, die an einer Schule in Essex Mathematik unterrichtet. Seit Mitte 2018 veröffentlicht sie alle paar Tage auf Twitter ein mathematisches Rätsel. Ihre Fan-Gemeinde ist in kürzester Zeit auf viele Tausend Mitglieder in der ganzen Welt gewachsen. Am 24. August 2019 stellte sie folgende Aufgabe:
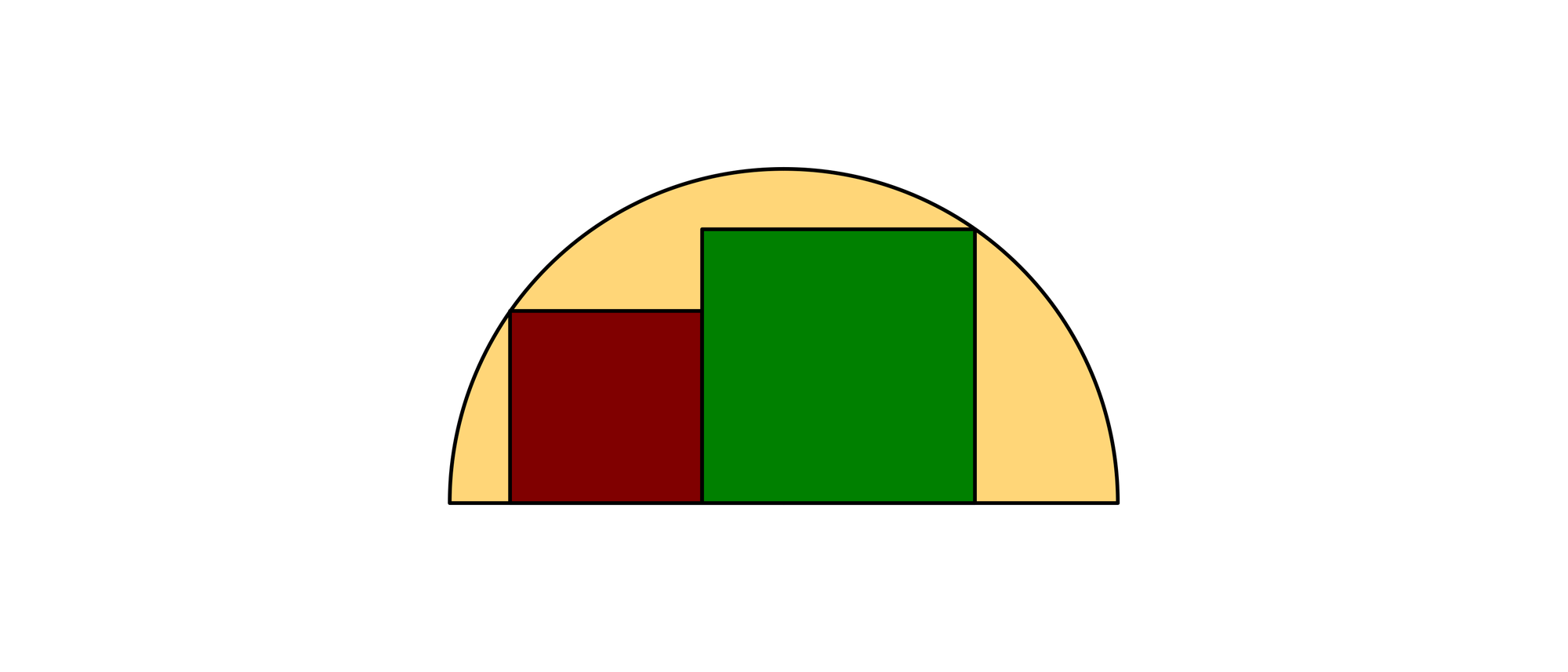
In einem Halbkreis mit dem Radius 8 liegen zwei Quadrate so, wie es das Bild zeigt. Das Verhältnis A1/A2 der Flächeninhalte der beiden Quadrate beträgt x. Wie groß ist die Summe A1 + A2 der beiden Flächeninhalte in Abhängigkeit von x?
Die Lösung ist nicht schwer zu finden, wenn man den Halbkreis mit dem Radius r und dem Mittelpunkt M zu einem Kreis mit vier Quadraten verdoppelt.
Haben das kleine und das große Quadrat die Seitenlängen a und b, gilt für die Hypotenuse des rechtwinkligen Dreiecksecks ABC nach dem Satz des Pythagoras c2 = (b + a)2 + (b − a)2. Dies lässt sich zu c2 = 2(a2 + b2) zusammenfassen.
Die Diagonale BD durch das obere rote und das untere grüne Quadrat schließt mit den Quadratseiten AD einen Winkel von α = 45° ein. Der Winkel β ist der Mittelpunktswinkel über demselben Bogen AB, über dem α ein Umfangswinkel ist. Folglich ist β = 2α = 90°.
Damit ist das Dreieck ABM auch rechtwinklig, und es gilt c2 = 2r2. Setzt man die beiden Gleichungen für c2 gleich, erhält man 2(a2 + b2) = 2r2 oder a2 + b2 = r2 = 64.
Das Verhältnis der Flächeninhalte der beiden Quadrate spielt dabei keine Rolle.
Schreiben Sie uns!
2 Beiträge anzeigen