Hemmes mathematische Rätsel: Wie groß ist die Summe der Umfänge aller Kreise?
Zwischen 1959 und 1964 warb die Firma Litton Industries in den Zeitschriften »Aviation Week« und »Electronic News« für ihre Produkte mit Anzeigen, die jedes Mal eine mathematische Denksportaufgabe enthielten. Diese Aufgaben waren ein so großer Erfolg, dass Litton Industries sie in gesammelter Form als eine Reihe kleiner Hefte mit dem Titel »Problematical Recreations« herausgab. Bei einem dieser Probleme geht es um eine Grenzwertberechnung.
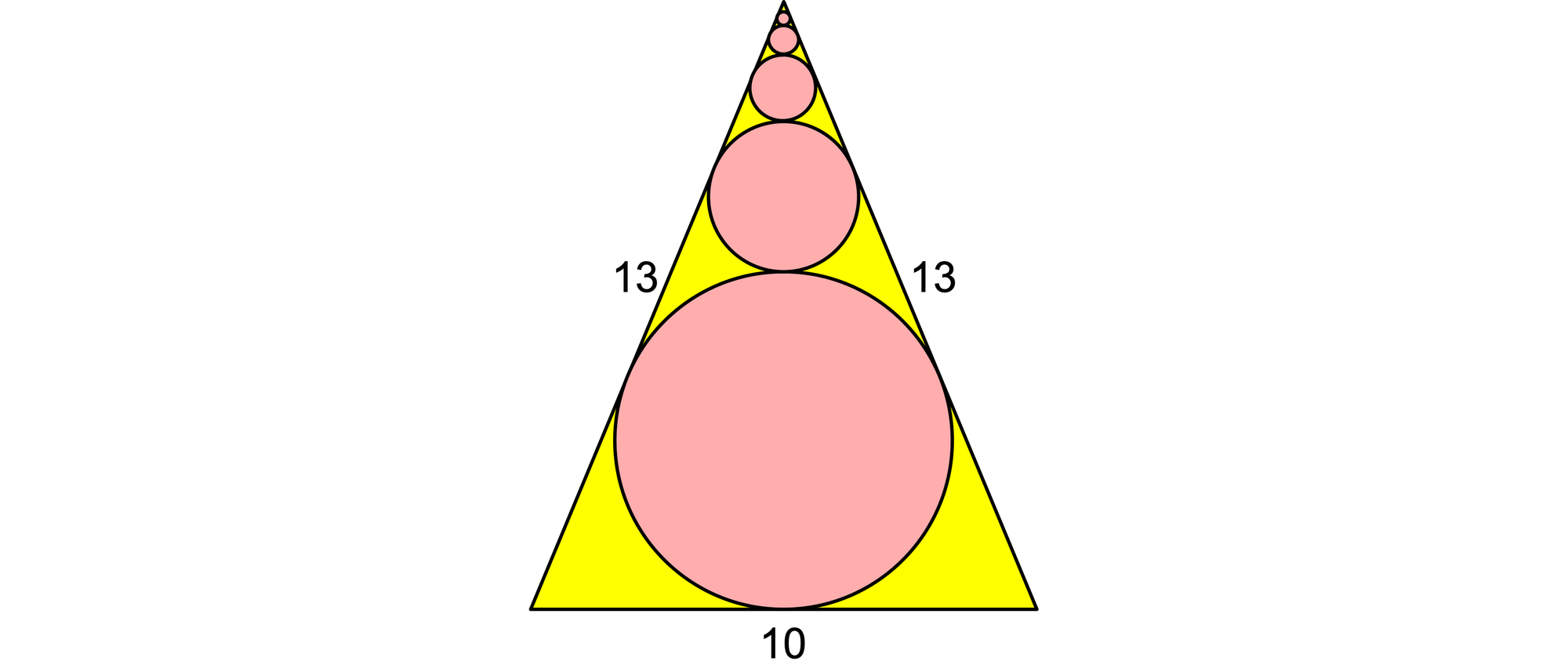
In ein gleichschenkliges Dreieck mit den Seitenlängen 13, 13 und 10 ist der Inkreis eingezeichnet und eine unendliche Folge weiterer Kreise, die jeweils die beiden gleichen Schenkel des Dreiecks und den nächstgrößeren und nächstkleineren Kreis berühren. Wie groß ist die Summe der Umfänge aller Kreise?
Ein mathematisch geschulter Verstand erkennt in dieser Aufgabe sofort eine unendliche Reihe und sucht mit Hilfe der Mathematik der Reihen die Lösung. Diese Methode führt zum Ziel, ist aber sehr unwirtschaftlich. Es geht auch viel einfacher. Für die Höhe des Dreiecks gilt nach dem Satz des Pythagoras h2 = 132 − 52. Damit erhält man h = 12.
Der Umfang eines Kreises ist gleich dem π-fachen seines Durchmessers, die Summe aller Umfänge ist gleich dem π-fachen der Summe aller Durchmesser. Die Summe aller Durchmesser ist aber gleich der Dreieckshöhe h. Somit beträgt die Summe alle Umfänge 12π ≈ 37,699.
Schreiben Sie uns!
Beitrag schreiben