Hemmes mathematische Rätsel: Wie groß sind die Felder des Bauern?
Henry Ernest Dudeney (1857–1930) war wohl der bedeutendste Rätselerfinder, der jemals lebte. Das folgende Problem veröffentlichte er am 25. Januar 1903 in der britischen Zeitung »The Weekly Dispatch«.
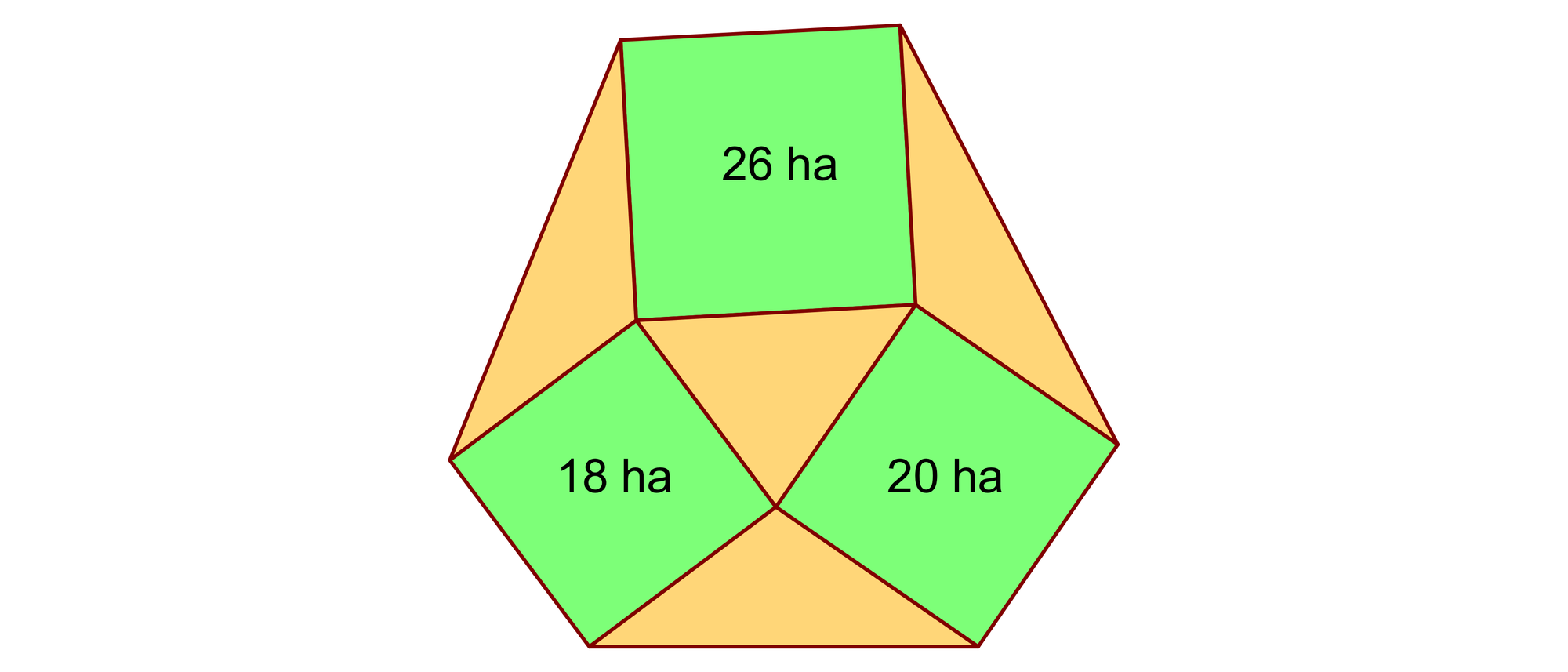
Ein Bauer besitzt drei 18, 20 und 26 Hektar große quadratische Felder, die ein dreieckiges Stück Land einschließen. Zwischen jedem Felderpaar liegt ein dreieckiges Stück Land. Eines Tages kauft der Bauer die vier dreieckigen Landstücke. Nun bilden seine Ländereien ein unregelmäßiges Sechseck. Wie viele Hektar misst es?
Da 26 = 12 + 52, 20 = 22 + 42 und 18 = 32 + 32 ist, kann man um das mittlere Dreieck drei rechtwinklige Dreiecke I, II und III legen, die als Hypotenusen die Seiten des mittleren Dreiecks haben.
Außerdem liegen die Ecken aller vier Dreiecke auf Kreuzungspunkten eines quadratischen Rasters, dessen Felder alle ein Hektar groß sind. Ergänzt man die Figur um die drei Quadrate und die drei äußeren Dreiecke, müssen auch deren Ecken alle auf Rasterpunkte fallen. In der Zeichnung liegen vier Ecken des Sechsecks auf Kreuzungspunkten eines Rasters von 12×12 = 144 Quadraten.
Zieht man von 144 Hektar die Flächen der beiden Rechtecke A und E und der sechs Dreiecke B, C, D, F, G und H ab, erhält man als Sechseckfläche 144 − 2 − 2 − (1×5 + 5×7 + 2×4 + 1×7 + 3×3 + 2×8)/2 = 100 Hektar.
Schreiben Sie uns!
Beitrag schreiben