Hemmes mathematische Rätsel: Wie groß ist die Seitenlänge der Quadrate?
In einem Rechteck mit den Seitenlängen 26 und 17 stecken sieben gleiche Quadrate. Wie groß ist die Seitenlänge der Quadrate?
© Heinrich Hemme (Ausschnitt)
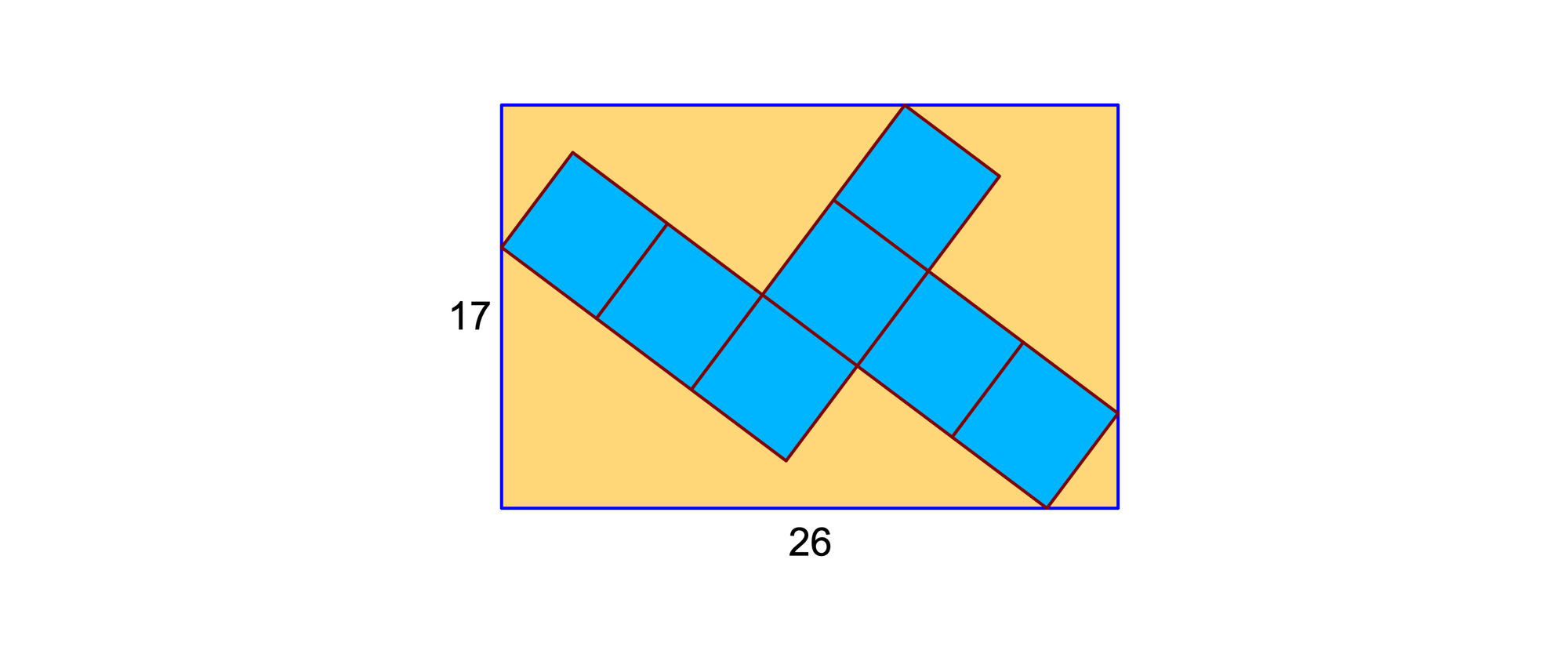
In einem Rechteck mit den Seitenlängen 26 und 17 stecken, so wie es das Bild zeigt, sieben gleiche Quadrate. Wie groß ist die Seitenlänge der Quadrate?
Der Schlüssel zur Lösung ist das kleine, rote, rechtwinklige Dreieck, das in der unteren, rechten Ecke des Rechtecks steckt und eine Quadratseite c als Hypotenuse hat, Seine Katheten haben die Längen a und b. Kopien dieses Dreiecks lassen sich so, wie es das Bild zeigt, in die sieben Quadrate setzen.
Nun sieht man, dass 2a + 5b = 26 und 3a + 2b = 17 ist. Diese beiden Gleichungen haben die Lösung a = 3 und b = 4. Daraus ergibt sich mit dem Satz des Pythagoras c2 = a2 + b2 = 25. Die Quadrate haben folglich die Seitenlänge 5.
© Heinrich Hemme
Schreiben Sie uns!
Beitrag schreiben