Rätseln mit Eder: Wie lang müssen a und b sein, damit das Volumen maximal ist?
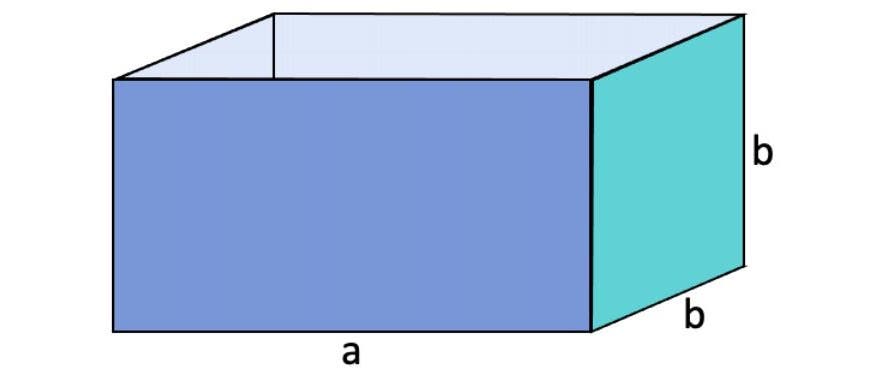
Eine Verpackungsfirma benötigt quaderförmige Schachteln aus Pappe, deren Höhe genauso lang ist wie die Seite b. Zusätzlich soll für a und b gelten: a + b = 45
Welche Längen müssen die natürlichen Zahlen a und b haben, damit das Volumen der Schachtel den größten Wert annimmt?
Wenn a = 15 cm und b = 30 cm lang sind, ist das Volumen der Schachtel mit 13 500 cm3 am größten.
Erklärung
Die Formel für das Volumen eines Quaders lautet V = Länge · Breite · Höhe, für die Aufgabe ist also V = a · b · b.
Der Wert für a + b = 45 war vorgegeben, und a und b sollten natürliche Zahlen sein. Somit kommen für a und b genau 44 Lösungsmöglichkeiten infrage.
1+44=45, 2+43=45, 3+42=45, ... , 42+3=45, 43+2=45,44+1=45.
Jetzt lässt sich mit diesen Möglichkeiten das jeweilige Volumen berechnen: V1=1·44·44=1936, V2=2·43·43=3698, V3=3·42·42=5292, ... Man erkennt, dass sich das Volumen für die verschiedenen Werte von a und b verändert.
Am größten ist der Wert für V15=15·30·30=13500.
Eine elegantere Lösung lässt sich mithilfe der Differentialrechnung finden. Diese wird in den Oberstufen der Gymnasien, Gesamtschulen und Berufskollegs behandelt. Im Video wird diese Lösungsvariante gezeigt.
Schreiben Sie uns!
Beitrag schreiben