Hemmes mathematische Rätsel: Wie können die beiden Dreiecke den gleichen Flächeninhalt haben?
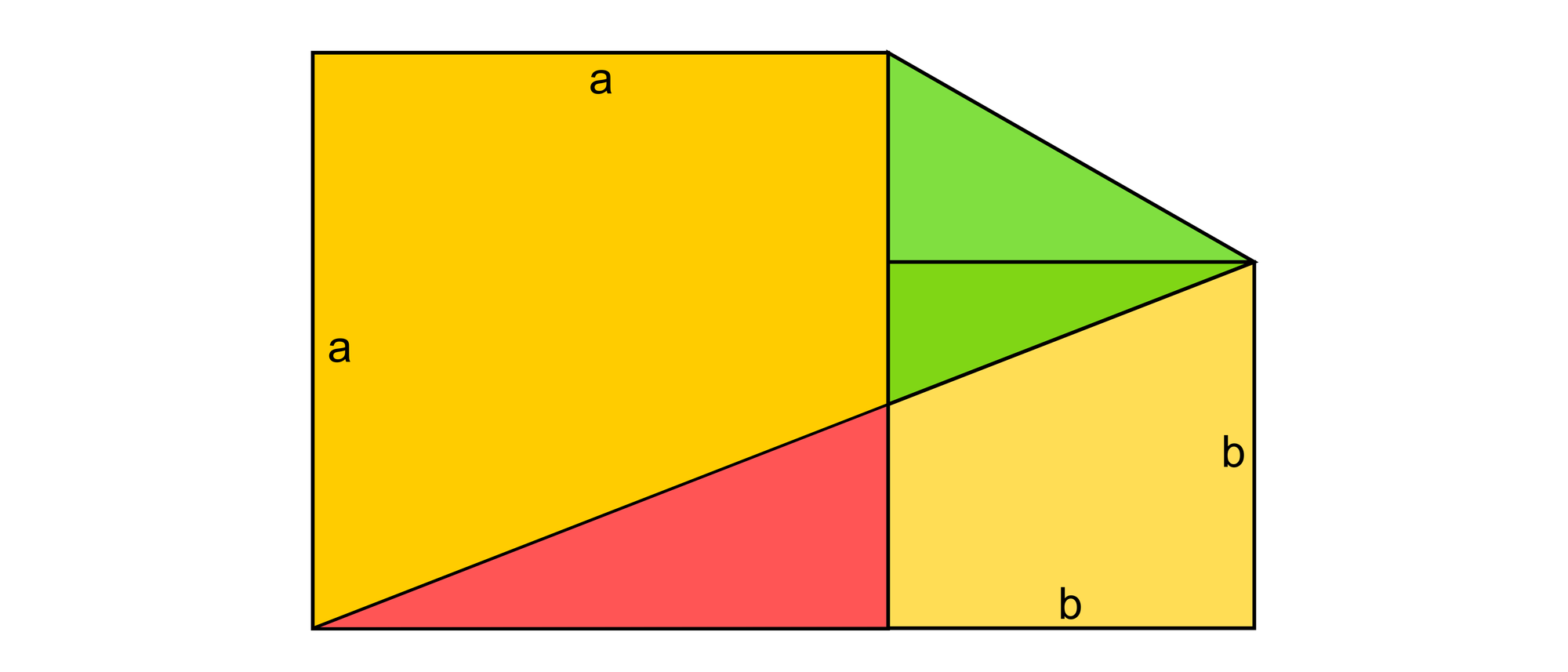
Das heutige Rätsel ist noch ganz neu und wurde Anfang 2023 von John Kruse aus Aachen erdacht. Zwei Quadrate mit den Seitenlängen a und b liegen so nebeneinander, wie es das Bild zeigt. Die rechte obere Ecke des rechten Quadrats wird durch zwei Strecken mit der linken unteren und der rechten oberen Ecke des linken Quadrats verbunden. Dadurch entstehen das rote und das grüne Dreieck. In welchem Verhältnis muss a zu b stehen, damit die beiden Dreiecke den gleichen Flächeninhalt haben?
In das rechte Quadrat wird die Diagonale BD gezeichnet. Dadurch entstehen die beiden Dreiecke ABD und EBD. Sie haben beide eine Grundseite der Länge a und eine Höhe der Länge b und somit den gleichen Flächeninhalt. Schneidet man nun von diesen beiden Dreiecken das Dreieck BDC ab, bleiben das rote Dreieck ABC und das grüne Dreieck CDE übrig, die dann natürlich auch den gleichen Flächeninhalt haben. Dabei spielt es keine Rolle, in welchem Verhältnis a zu b steht. Es braucht nicht einmal, wie in dem Bild, a > b zu sein, sondern es darf auch a = b oder a < b sein.
Schreiben Sie uns!
Beitrag schreiben