Hemmes mathematische Rätsel: Wie lässt sich das Verhältnis der Flächeninhalte bestimmen?
Im Januar 2024 veröffentlichte Manfred Pietsch aus Kreuzau in Nordrhein-Westfalen in der Aachener Zeitung ein hübsches Problem der ebenen Geometrie.
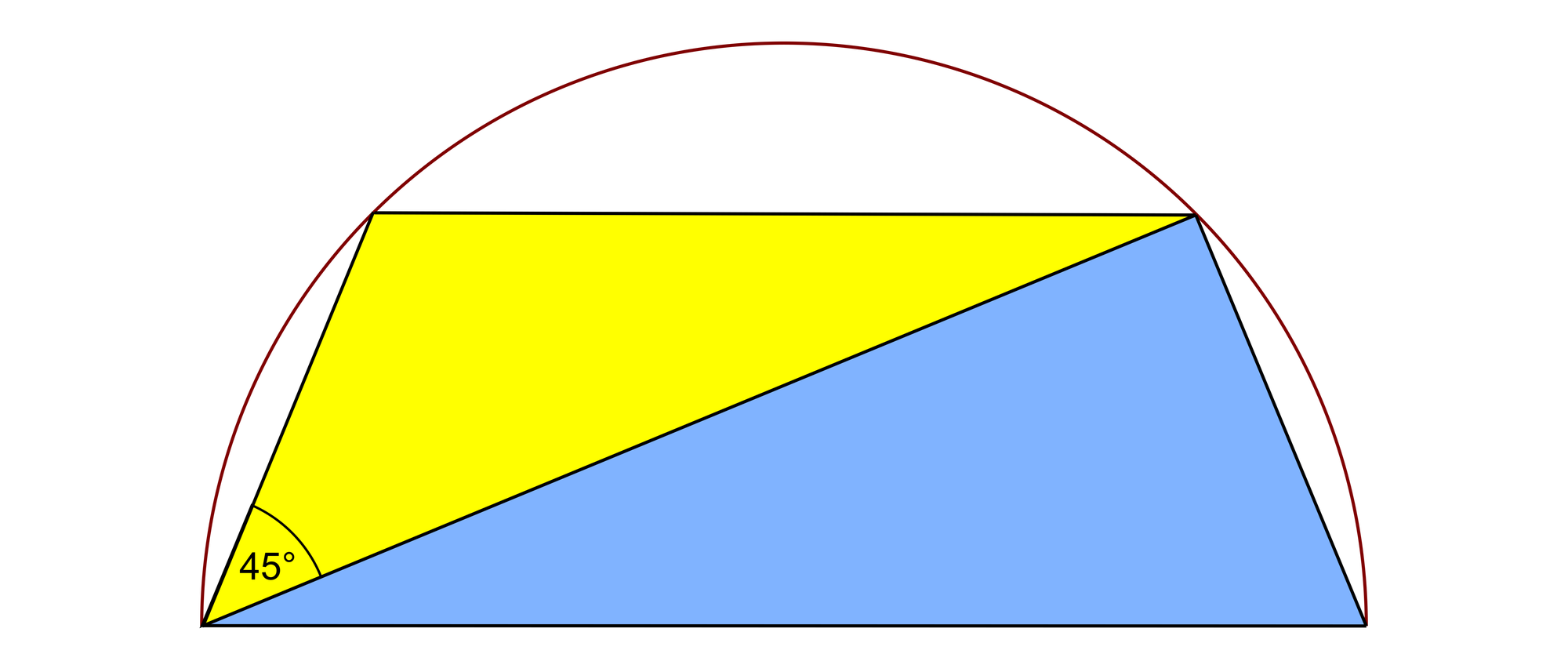
Ein gleichschenkliges Trapez liegt so in einem Halbkreis, wie es das Bild zeigt. Das Trapez wird durch eine seiner beiden Diagonalen in ein gelbes und ein blaues Dreieck geteilt. Der untere Winkel des gelben Dreiecks ist 45° groß. In welchem Verhältnis steht der Flächeninhalt des blauen Dreiecks zu dem des gelben Dreiecks?
Die beiden Diagonalen des Trapezes ABCD schneiden sich im Punkt S. Wegen der Symmetrie der Figur sind die beiden Dreiecke ABD und BAC Spiegelbilder voneinander und haben nach dem Satz des Thales bei D und C rechte Winkel. Da der Winkel SAD eine Größe von 45° hat, ist das Dreieck ASD rechtwinklig und gleichschenklig. Wegen der Symmetrie der Figur gilt dies auch für das Dreieck SBC. Ist a die Länge der Katheten und h die der Hypotenusenhöhe des Dreiecks ASD, gilt nach dem Satz des Pythagoras a = h√2. Die Diagonale AC ist die gemeinsame Grundseite des blauen und des gelben Dreiecks. Darum stehen die Flächeninhalte der beiden Dreiecke im gleichen Verhältnis wie ihre Höhen. Somit gilt Fblau : Fgelb = CB : DT = a : h = h√2 : h = √2 : 1.
Schreiben Sie uns!
1 Beitrag anzeigen