Hemmes mathematische Rätsel: Wie lässt sich der Flächeninhalt ermitteln?
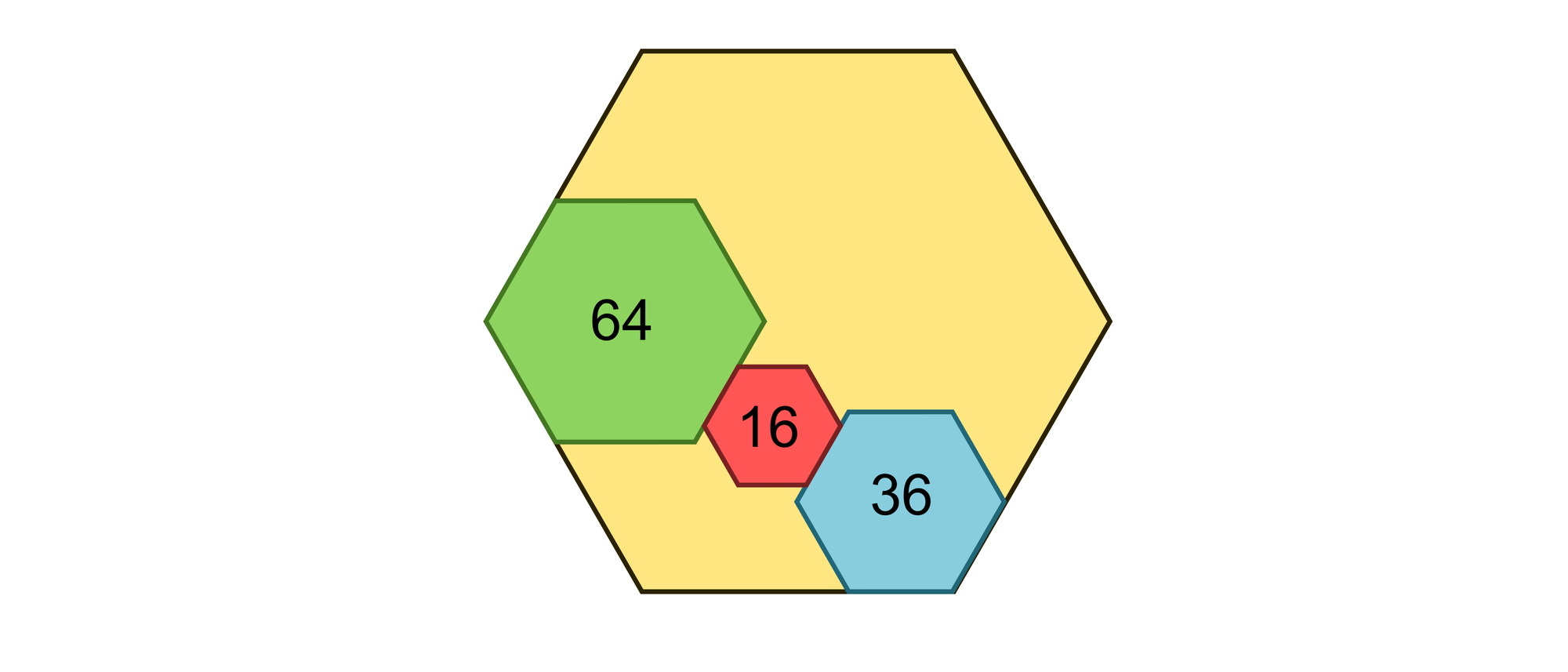
Das folgende Rätsel wurde 2023 von Manfred Pietsch aus Kreuzau in Nordrhein-Westfalen entworfen. Eine Kette von drei kleinen regelmäßigen Sechsecken verbindet, so wie es das Bild zeigt, zwei Ecken eines großen regelmäßigen Sechsecks. Welchen Flächeninhalt besitzt das große Sechseck, wenn die Inhalte der drei kleinen Sechsecke 64, 16 und 36 sind?
Das rote Sechseck wird so weit nach links unten verschoben, bis zwei seiner Ecken, so wie es das Bild zeigt, mit einer Ecke des grünen und einer des blauen Sechsecks zusammenfallen. Der kleine Durchmesser AB des großen Sechsecks setzt sich nun aus je einem kleinen Durchmesser des grünen, des roten und des blauen Sechsecks zusammen. Da die Flächen der drei kleinen Sechsecke im Verhältnis 64 : 16 : 36 stehen, stehen ihre kleinen Durchmesser im Verhältnis √64 : √16 : √36 oder 8 : 4 : 6. Somit stehen die kleinen Durchmesser des großen Sechsecks und des blauen Sechsecks im Verhältnis (8 + 4 + 6) : 6 = 18 : 6 = 3 : 1. Daraus ergibt sich für das Verhältnis der Fläche X des großen Sechsecks und der des blauen Sechsecks X : 36 = 32 : 12, was man zu X = 324 auflösen kann.
Schreiben Sie uns!
4 Beiträge anzeigen