Hemmes mathematische Rätsel: Wie lässt sich der Gesamtflächeninhalt bestimmen?
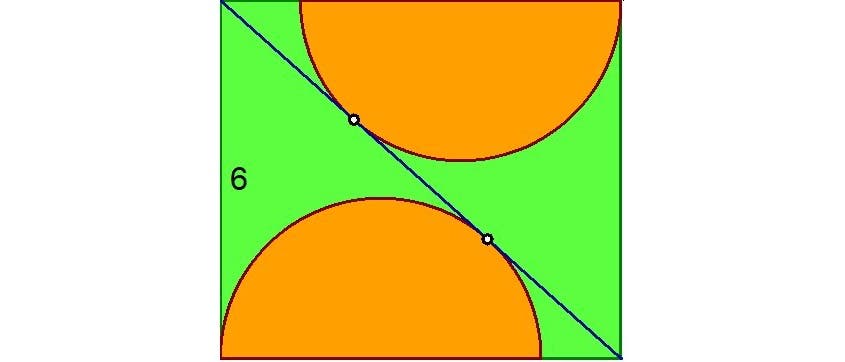
In einem Rechteck, dessen kurze Seite die Länge 6 hat, liegen zwei Halbkreise. Die beiden Halbkreise berühren eine Diagonale des Rechtecks, und die zwei Berührpunkte teilen die Diagonale in drei gleich lange Abschnitte. Wie groß ist der Gesamtflächeninhalt der beiden Halbkreise?
Die beiden rechtwinkligen Dreiecke ABC und ABD haben eine gemeinsame Hypotenuse und beide eine Kathete der Länge r. Folglich sind sie deckungsgleich, und die zweite Kathete hat die Länge 6. Außerdem haben die drei Diagonalenabschnitte jeweils die Länge 3. Überzieht man das Rechteck mit einem 3×3-Raster, haben seine Felder die Breite 2 und die Länge x. Für das Dreieck DEF erhält man mit dem Satz des Pythagoras 22 + x2 = 32 oder x = √5. Nun wendet man den Satz des Pythagoras auch noch auf das rechtwinklige Dreieck ADF an und bekommt r2 + 32 = (3x – r)2, woraus mit x = √5 die Gleichung r2 + 32 = (3√5 – r)2 wird. Löst man sie auf, erhält man r = 6/√5. Daraus ergibt sich ein Gesamtflächeninhalt der beiden Halbkreise von πr2 = 36π/5 ≈ 22,62.
Schreiben Sie uns!
Beitrag schreiben