Hemmes mathematische Rätsel: Wie lässt sich der Inhalt der Fläche bestimmen?
Catriona Agg ist eine britische Lehrerin, die seit 2018 alle paar Tage auf Twitter ihren Lesern ein mathematisches Rätsel stellt. Das heutige veröffentlichte sie 2020.
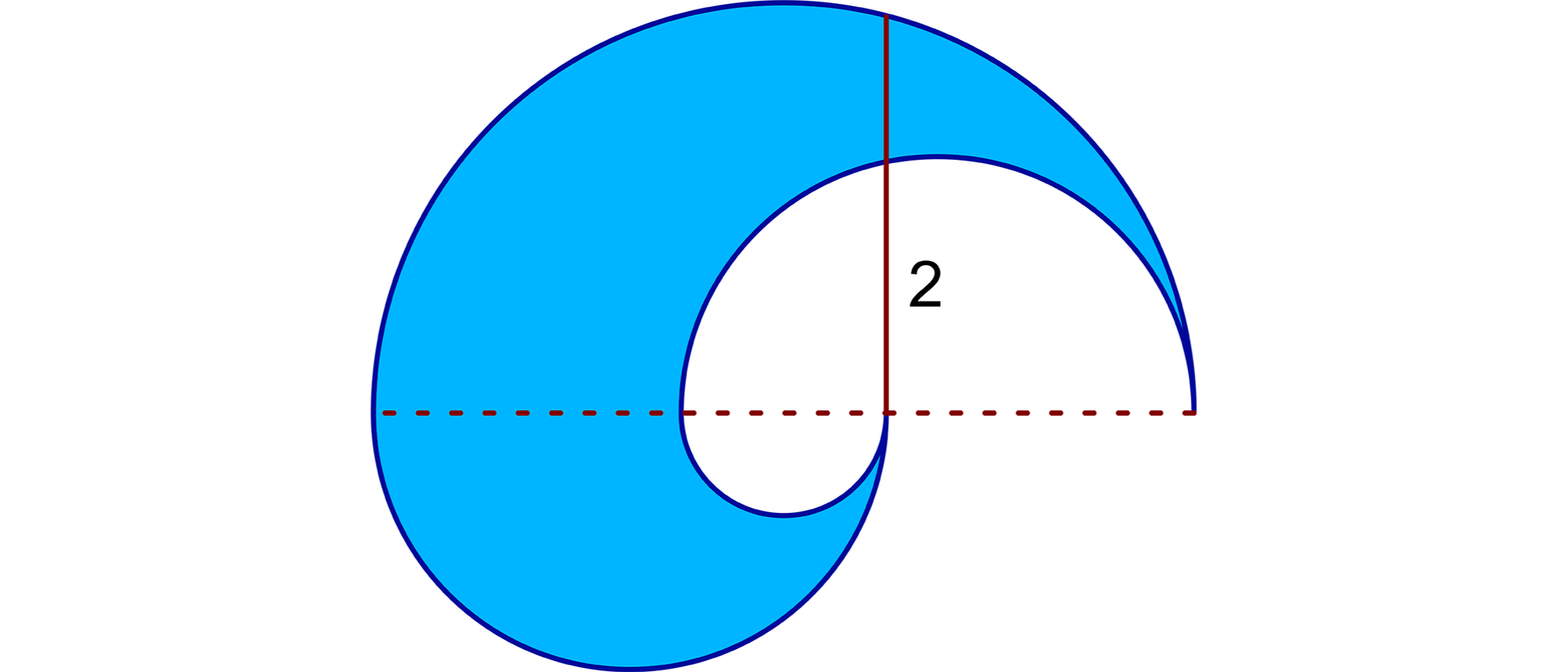
Vier Halbkreise hängen so aneinander, wie es das Bild zeigt. Der größte und der kleinste Halbkreis haben einen gemeinsamen Mittelpunkt. Die ausgezogene Strecke, die senkrecht zur gestrichelten Strecke steht, ist 2 lang. Wie groß ist der Inhalt der blauen Fläche?
Dreht man die beiden unteren Halbkreise um den Mittelpunkt des kleinen Kreises um 180°, entsteht ein halber Kreisring mit dem Innenradius r und dem Außenradius R. Mit dem Satz des Pythagoras erhält man R2 = 22 + r2 oder R2 – r2 = 4. Die Fläche des halben Kreisrings beträgt πR2/2 – πr2/2 = π(R2 – r2)/2, woraus mit dem zuvor erhaltenen Ausdruck 4π/2 = 2π ≈ 6,28 wird.
Schreiben Sie uns!
1 Beitrag anzeigen