Hemmes mathematische Rätsel: Wie lässt sich der Prozentsatz herausfinden?
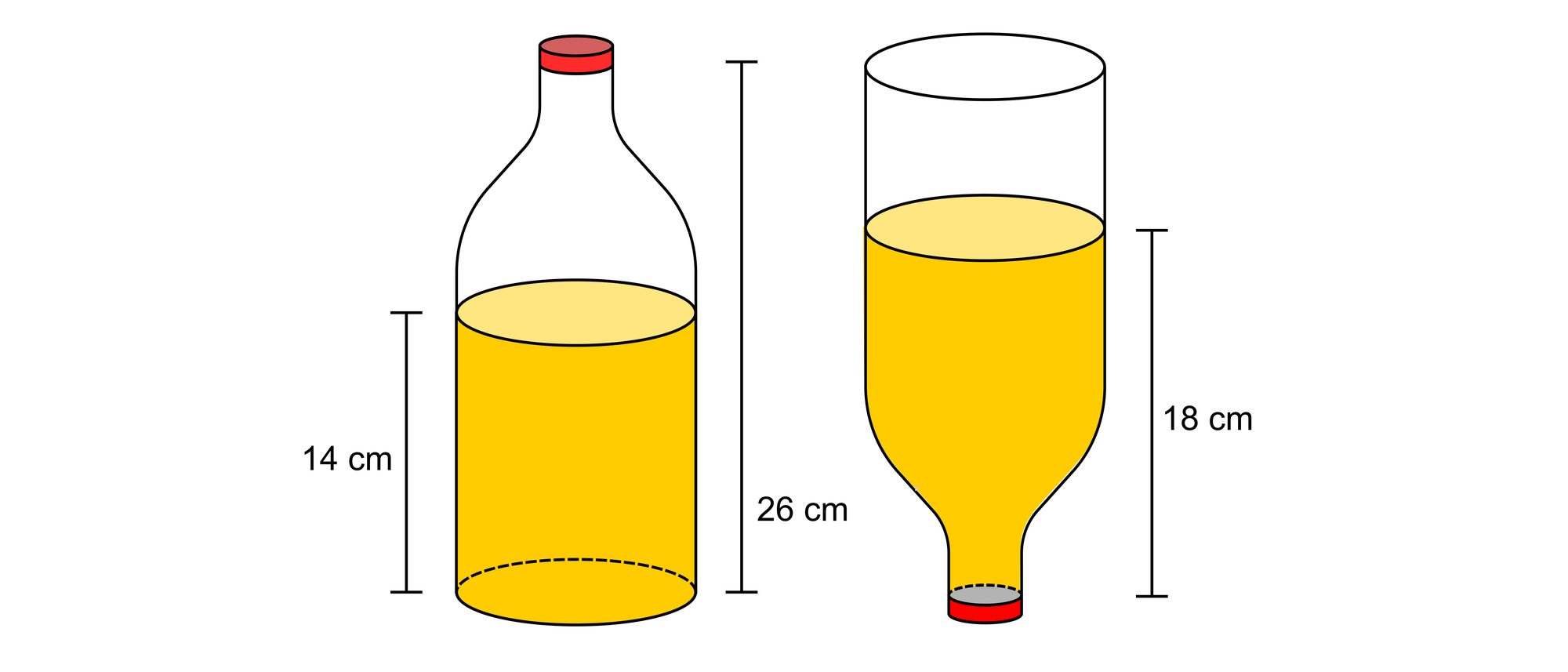
Eine Milchflasche hat einen flachen Boden und ist im unteren Teil zylindrisch. Erst im oberen Teil verschlankt sie sich. Ihr Innenraum ist vom Boden bis zum Verschluss 26 Zentimeter hoch. Die Flasche ist nicht vollständig mit Milch gefüllt, sondern nur bis zu einer Höhe von 14 Zentimetern. Stellt man die Flasche auf den Kopf, liegt der Spiegel der Milch 18 Zentimeter über der Innenseite des Verschlusses. Zu wie viel Prozent ist die Flasche mit Milch gefüllt?
Die leeren Bereiche haben bei der aufrecht und bei der kopfstehenden Flasche das gleiche Volumen. Würde man die Milch in einen zylinderförmigen Behälter füllen, der das gleiche Volumen wie die Flasche und den gleichen Querschnitt wie ihr Boden hat, wäre dieser bis in 14 Zentimeter Höhe mit Milch gefüllt, und darüber befände sich ein 26 cm – 18 cm = 8 cm hoher Leerraum. Der Behälter hätte also einen Innenraum von 14 cm + 8 cm = 22 cm Höhe. Er wäre somit ebenso wie die Flasche zu 14/22 = 7/11 ≈ 64 Prozent gefüllt.
Schreiben Sie uns!
1 Beitrag anzeigen