Hemmes mathematische Rätsel: Wie lässt sich die Größe des Radius bestimmen?
Presh Talwalkar hat Mathematik und Wirtschaftswissenschaften an der Stanford University in Kalifornien in den USA studiert. Er hat einige Bücher über mathematische Knobeleien und Kuriositäten geschrieben, darunter das im Jahr 2015 erschienene dreibändige Werk »Math Puzzles« und die ebenfalls 2015 erschienenen Bücher »40 Paradoxes in Logic, Probability, and Game Theory« und »The Best Mental Math Tricks«. Talwalkar betreibt auch im Internet seit 2007 den Denksport-Blog »Make Your Decision«. Am 21. November 2022 stellte er seinen Lesern und Leserinnen auf seiner Internetseite ein kniffliges Problem aus der ebenen Geometrie. Es stammt ursprünglich, wenn auch mit anderen Zahlenwerten, aus dem »JEE Advanced« des Jahres 2022 und war dort die Aufgabe 8 des Mathematikteils. Das »JEE Advanced« ist eine sehr anspruchsvolle Prüfung für die Zulassung zu den renommierten IIT-Schulen in Indien.
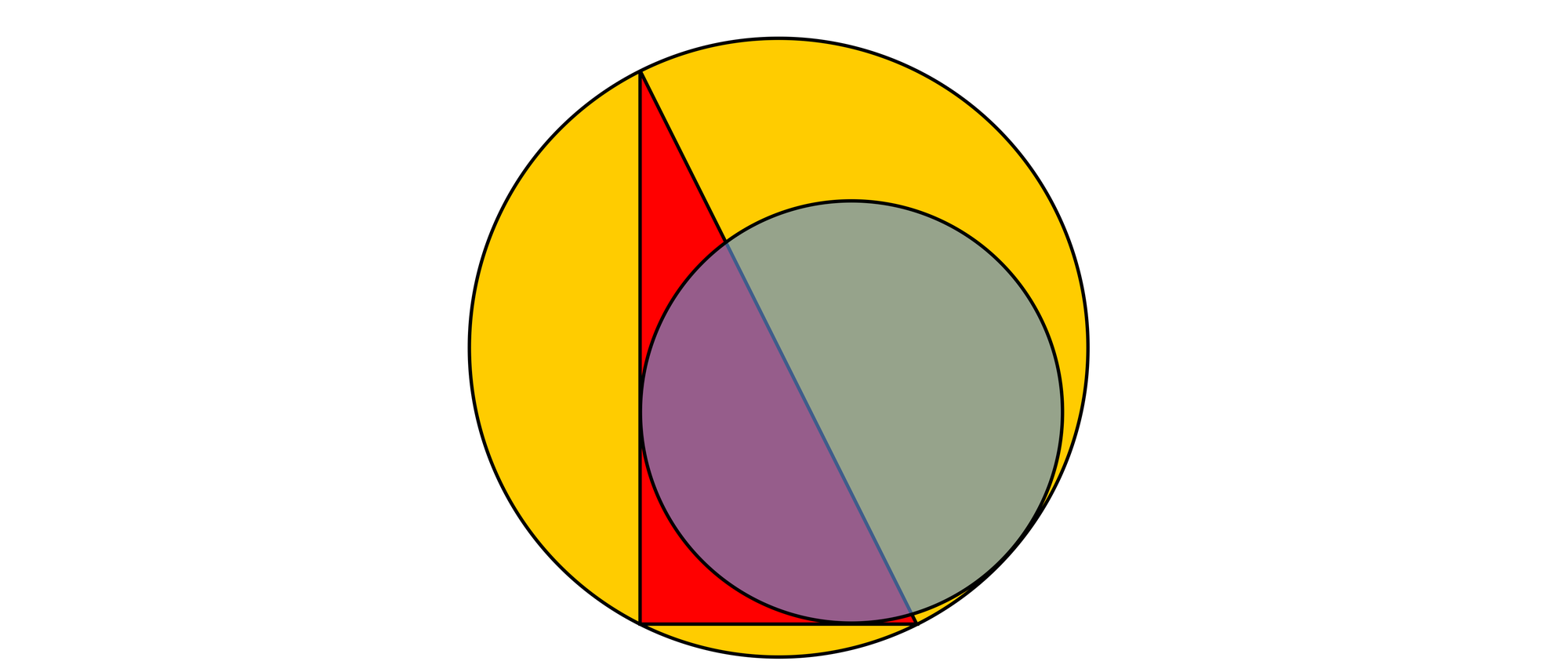
Die Ecken eines rechtwinkligen Dreiecks, dessen Katheten die Längen 2 und 4 haben, liegen auf dem Umfang eines großen Kreises. Ein kleiner Kreis berührt den großen Kreis und die beiden Katheten des Dreiecks. Wie groß ist der Radius des kleinen Kreises?
M und N sind die Mittelpunkte und R und r die Radien des äußeren und des inneren Kreises. Da bei einem Kreis der Radius immer senkrecht auf den Umfang trifft, liegen die beiden Mittelpunkte M und N und der Berührpunkt E der beiden Kreise auf einer Geraden. Für das rechtwinklige Dreieck ABC mit den Seiten a = 4, b = 2 und c gilt nach dem Satz des Pythagoras a2 + b2 = c2. Da der Außenkreis ein Thaleskreis des Dreiecks ABC ist, fällt sein Mittelpunkt auf den Mittelpunkt der Hypotenuse. Somit ist R = c/2 = 1/2√(a2 + b2) = √5. Die Katheten der rechtwinkligen Dreiecke NMD und ABC liegen parallel zueinander. Für die Seiten des Dreiecks NMD gilt x = a/2 – r = 2 – r, y = r – b/2 = r – 1 und z = R – r = √5 – r und außerdem nach dem Satz des Pythagoras x2 + y2 = z2. Setzt man diese Gleichungen ineinander ein, erhält man (r – 1)2 + (2 – r)2 = (√5 – r)2, was man zu r = 2(3 – √5) ≈ 1,5279 auflösen kann. Der Radius des kleinen Kreises hat also eine Länge von etwa 1,5279.
Schreiben Sie uns!
Beitrag schreiben