Hemmes mathematische Rätsel: Wie lässt sich dieses Kreuzzahlrätsel lösen?
David Wells wurde 1940 in England geboren. Er studierte Mathematik an der Universität Cambridge, brach aber sein Studium ab und ließ sich danach zum Lehrer ausbilden. Während seines Studiums wurde er britischer Schachmeister der Spieler, die noch keine 21 Jahre alt waren. Er hat zahlreiche Knobeleien erfunden und betreute in den siebziger Jahren die Denksportredaktion der Zeitschrift „Games and Puzzles“. Von 1981 bis 1983 gab er eine eigene Zeitschrift heraus mit dem Titel „The Problem Solver“. Wells hat etliche Bücher zur Unterhaltungsmathematik geschrieben. Die heutige Kopfnuss stammt aus seinem 1984 erschienenen Büchlein „Can You Solve This?, Series 2“.
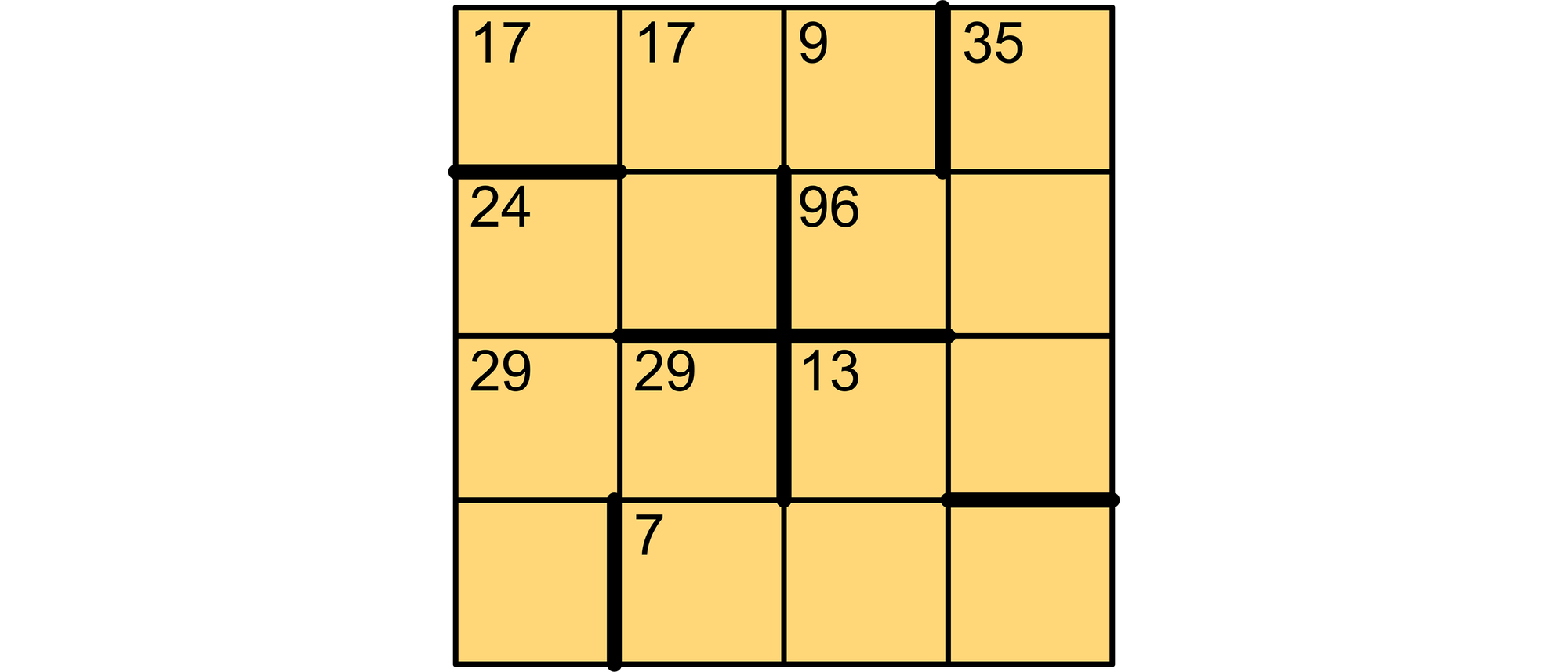
Setzen Sie in jedes Feld dieses Kreuzzahlrätsels eine Ziffer. Die zwei- und dreistelligen Zahlen, die dadurch waagerecht und senkrecht entstehen, sollen ganzzahlige Vielfache der kleinen Zahlen sein, die jeweils in ihrem ersten Feld oben links stehen.
Das einzige zweistellige Vielfache von 96 ist 96 selbst. Folglich ist die zweite Zahl der zweiten Zeile 96. Da nur 11 · 9 = 99 auf 9 endet, muss die erste Zahl in der dritten Spalte 99 sein. Die dreistellige Zahl in der vierten Spalte ist ein Vielfaches von 35 und kann deshalb nur auf 0 oder 5 enden. Somit muss auch die zweite Zahl in der dritten Zeile, die ein Vielfaches von 13 ist, auf 0 oder 5 enden. Dafür kommt nur 65 in Frage. Damit muss auch die zweite Zahl in der dritten Spalte 65 sein. Die einzige dreistellige Zahl für die vierte Spalte, die durch 35 teilbar ist und auf 65 endet, ist 665. Die zweistelligen Vielfachen von 29 sind 29, 58 und 87. Daraus ergibt sich sofort, dass die erste Zahl der dritten Zeile 58 und die zweite Zahl der zweiten Spalte 87 sein muss. Die zweistelligen Vielfachen von 17 sind 17, 34, 51, 68 und 85 und die von 24 sind 24, 48, 72 und 96. Somit sind die ersten Zahlen der zweiten Spalte und Zeile entweder 34 und 24 oder 68 und 48. Darum kann die dreistellige Zahl der ersten Zeile entweder auf 39 oder 69 enden. Nur im zweiten Fall erhält man eine durch 17 teilbare Zahl, nämlich 969. Der Rest ist einfach.
Schreiben Sie uns!
Beitrag schreiben