Hemmes mathematische Rätsel: Wie lang ist der untere Teil?
Presh Talwalkar hat Mathematik und Wirtschaftswissenschaften an der Stanford University in Kalifornien in den USA studiert. Er hat einige Bücher über mathematische Knobeleien geschrieben, darunter das im Jahr 2015 erschienene dreibändige Werk »Math Puzzles«. Talwalkar betreibt auch im Internet seit 2007 den Denksport-Blog »Mind Your Decisions«. Am 17. Januar 2023 stellte er seinen Lesern und Leserinnen auf seiner Seite ein kniffliges geometrisches Problem, das ihm von jemandem namens Kevin zugesandt worden war.
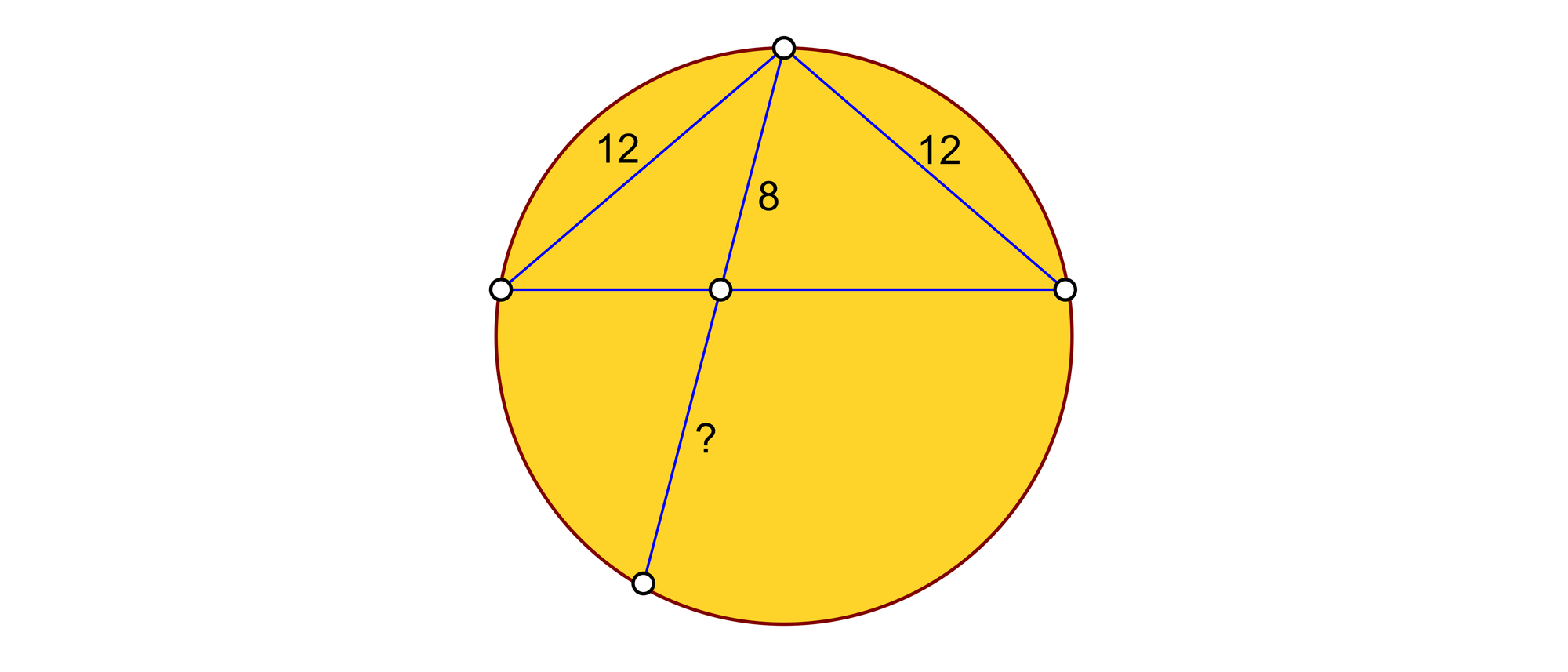
Durch einen Kreis laufen, so wie es das Bild zeigt, vier Sehnen. Zwei davon haben die Länge 12. Die beiden anderen Sehnen schneiden sich. Der obere Teil der von oben nach unten laufenden Sehne hat die Länge 8. Wie lang ist ihr unterer Teil?
Wir ergänzen die Zeichnung um eine fünfte Sehne CD. Das Dreieck ABC ist gleichschenklig. Deshalb sind seine Winkel CBA und ACB gleich groß. Da die Winkel CBA und CDA Umfangswinkel über demselben Kreisbogen CA sind, haben auch sie die gleiche Größe. Somit haben die beiden Dreiecke AEC und CAD gleiche Winkel und sind folglich ähnlich. Darum gilt für die Verhältnisse der einander entsprechenden Seitenlängen AD/AC = AC/AE oder AD/12 = 12/8. Dies lässt sich zu AD = 18 auflösen. Somit ist ED = 10.
Schreiben Sie uns!
Beitrag schreiben