Hemmes mathematische Rätsel: Wie lang ist die mittlere Sehne?
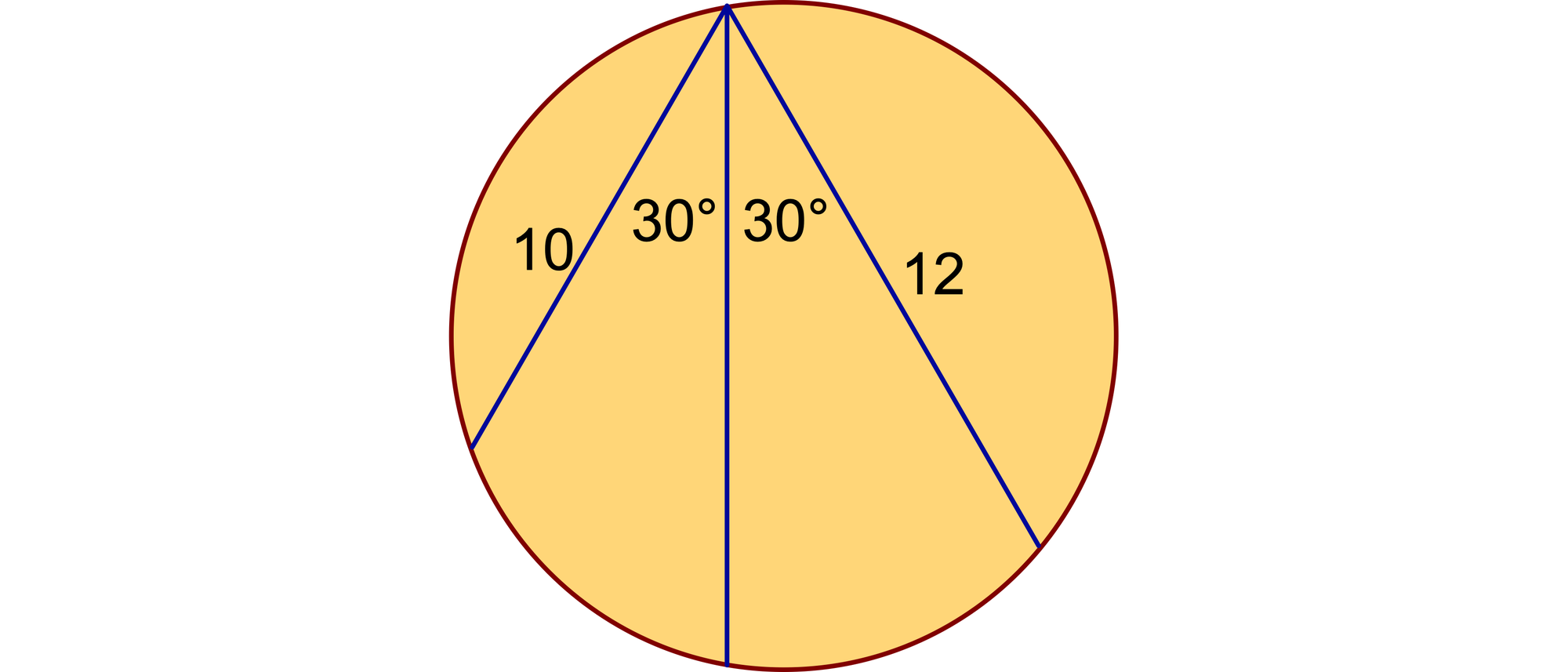
Drei Sehnen treffen sich in einem Punkt auf einem Kreisumfang. Die linke und die rechte Sehne haben die Längen 10 und 12 und schließen mit der mittleren Sehne jeweils einen Winkel von 30 Grad ein. Wie lang ist die mittlere Sehne?
Die beiden Winkel BAC und BDC sind Umfangswinkel über demselben Bogen BC und somit gleich groß. Auch die beiden Winkel CAD und CBD sind Umfangswinkel über demselben Bogen CD und folglich gleich groß. Die beiden Winkel BDC und CBD sind also 30° groß. Damit ist das Dreieck BCD gleichschenklig und die Sehnen BC und CD haben beiden die Länge y.
Mit dem Kosinussatz erhält man für die beiden Dreiecke ABC und ACD die Gleichungen y2 = 102 + x2 − 2 · 10 · x · cos 30° und y2 = 122 + x2 − 2 · 12 · x · cos 30°, die sich zu y = 100 + x2 − 20x cos 30° und y = 144 + x2 − 24x cos 30° zusammenfassen lassen.
Nun werden sie gleichgesetzt und ergeben 100 + x2 − 20x cos 30° = 144 + x2 − 24x cos 30° oder x = 44/cos 30° = 22/√3 ≈ 12,702.
Schreiben Sie uns!
4 Beiträge anzeigen