Hemmes mathematische Rätsel: Wie lang ist die Strecke x?
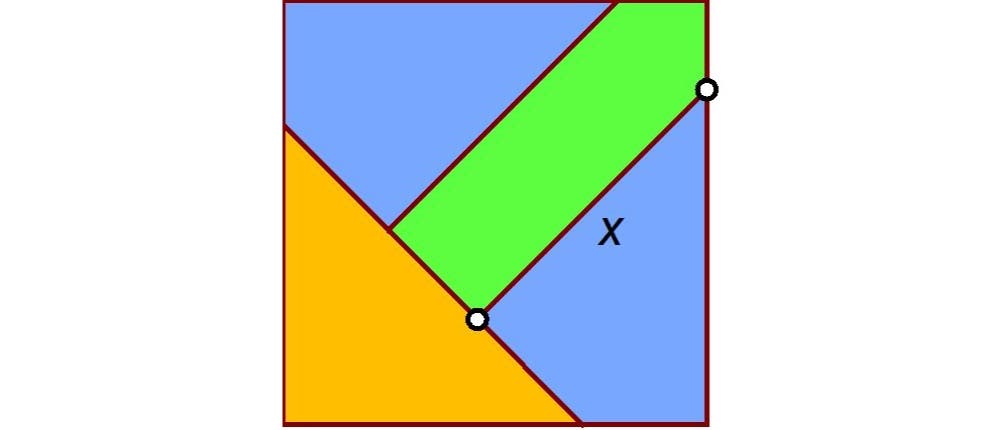
Ein Quadrat wird, wie es das Bild zeigt, in ein gleichschenkliges Dreieck mit einem rechten Winkel, in zwei Vierecke mit je zwei rechten Winkeln und in ein Fünfeck mit drei rechten Winkeln geteilt. Das Dreieck, die beiden Vierecke und das Fünfeck haben jeweils einen Flächeninhalt von 1. Wie lang ist die Strecke x?
Die vier Teile des Quadrats haben jeweils einen Flächeninhalt von 1. Darum hat das Quadrat ABCD selbst den Flächeninhalt 4 und die Seitenlänge 2. Das Dreieck AEH ist rechtwinklig, gleichschenklig und hat den Flächeninhalt 1. Folglich haben seine Katheten AE und AH die Länge √2. Verlängert man die Strecken IE und FB nach unten, schneiden sie sich im Punkt K und es entstehen die beiden rechtwinkligen, gleichschenkligen Dreiecke KBE und FIK. Das Dreieck KBE hat die Kathetenlänge EB = AB – AE = 2 – √2, und darum den Flächeninhalt 1/2(2 – √2)2 = 3 – 2√2. Das Dreieck FIK hingegen hat die Kathetenlänge IK = x, und darum den Flächeninhalt 1/2x2. Da das Dreieck FIK sich aus dem Viereck FIEB und dem Dreieck KBE zusammensetzt, gilt für seine Fläche 1/2x2 = 1 + (3 – 2√2). Daraus erhält man x = 2√(2 – √2) ≈ 1,531.
Schreiben Sie uns!
1 Beitrag anzeigen