Hemmes mathematische Rätsel: Wie lang muss das Stoffstück sein?
Klaus Bullerschen von der Fachhochschule Aachen erdachte 2004 eine kleine Knobelei über eine Teppichwendel und veröffentlichte sie noch im selben Jahr in den »Aachener Nachrichten« und in der »Aachener Zeitung«.
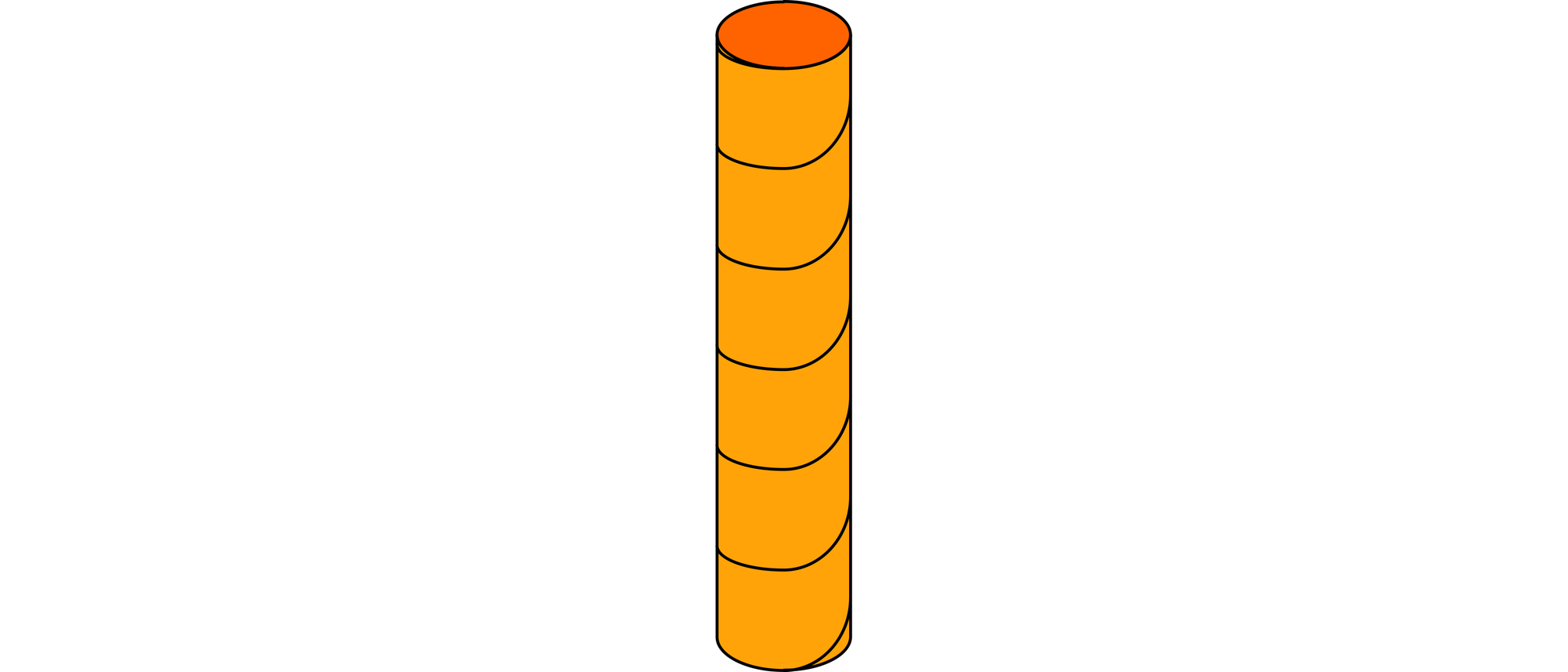
Herr Kleinlich besitzt eine Doppelgarage, die in der Mitte durch eine Säule abgestützt wird. Leider hat er sich beim Öffnen seines Autos an ihr schon manche Beule in die Tür gestoßen. Deshalb möchte er die Säule mit einem langen Streifen Teppichboden wendelförmig umkleben. Dabei soll der Teppichboden sich weder überlappen noch Stellen der Säule unbedeckt lassen.
Die Säule ist 2,40 m hoch und hat einen Umfang von 50 cm. In einem Fachgeschäft findet er einen langen, 30 cm breiten Reststreifen Teppichboden. Ein wie langes Stück muss er davon kaufen? Natürlich gibt es an beiden Enden etwas Verschnitt, wenn er den Streifen um die Säule klebt.
Um die Aufgabe zu lösen, rollt man die Säule soweit über den Boden, bis sich der Teppichstreifen ganz abgewickelt hat. Da der Streifen die Säule lückenlos umwendelt hat, schneiden seine beiden Ränder die Unterkante der Säule im Abstand ihres Umfangs u. Für die beiden dreieckigen Verschnittstücke gilt nach dem Satz des Pythagoras c2 = u2 − b2. Mit u = 50 cm und b = 30 cm erhält man daraus c = 40 cm. Die beiden Dreiecke A und B sind ähnlich. Folglich ist a : h = u : b. Hieraus ergibt sich a = uh/b = 400 cm. Der Teppichstreifen hat somit eine Länge von a + c = 440 cm.
Schreiben Sie uns!
Beitrag schreiben