Wie man ein Dreieck auch halbieren kann
© Norbert Treitz (Ausschnitt)
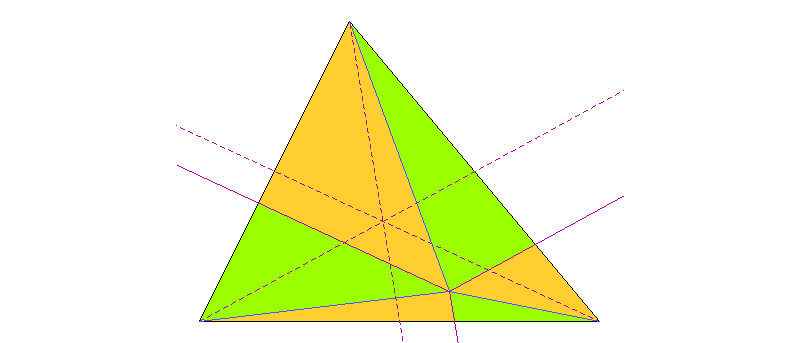
Von einem beliebigen Punkt im Inneren eines beliebigen Dreiecks werden die Geraden zu den Ecken und die Parallelen zu den Seitenhalbierenden zu den entsprechenden Seiten (also zu den Medianen) gezogen. Die sechs Flächen werden abwechselnd grün und orange gefärbt. Warum bekommt dabei jede Farbe genau die Hälfte der gesamten Fläche?
Ziehen Sie auch Parallelen zu den Seiten durch den Punkt.
© Norbert Treitz (Ausschnitt)
Die roten Linien sind die Parallelen der Dreiecksseiten durch den Punkt. Wir arbeiten uns nun von unten nach oben, um zu zeigen, dass jeweils aneinandergrenzende rote und grüne Dreiecke die gleiche Fläche haben:
- Unten links: Das dunkelgrüne und das dunkelrote Dreieck bilden zusammen ein Parallelogramm. Darum sind ihre Flächen gleich.
- Unten rechts: Auch hier bilden das dunkelgrüne und das dunkelrote Dreieck ein Parallelogramm. Auch deren Flächen sind also gleich groß.
- Unten Mitte: Das hellgrüne und das hellrote Dreieck bilden zusammen ein etwas größeres Dreieck, das dem ursprünglichen Dreieck ähnlich ist. Darum ist auch die Parallele zur Seitenhalbierenden des ursprünglichen Dreiecks im kleinen Dreieck eine Seitenhalbierende. Deshalb müssen das hellrote und hellgrüne Dreieck die gleiche Fläche besitzen.
- Oben links: Auch hier bilden das hellgrüne und das hellrote Dreieck ein neues Dreieck, das ähnlich zum ursprünglichen ist. Somit haben sie ebenfalls die gleiche Fläche.
- Oben rechts: Hier gilt genau das gleiche wie zuvor für das hellrote und das hellgrüne Dreieck.
- Oben Mitte: Das dunkelgrüne und das dunkelrote Dreieck bilden ein Parallelogramm. Auch ihre Flächen sind damit gleich.
Schreiben Sie uns!
Beitrag schreiben