Hemmes mathematische Rätsel: Wie müssen diese Zahlen auf den Stern verteilt werden?
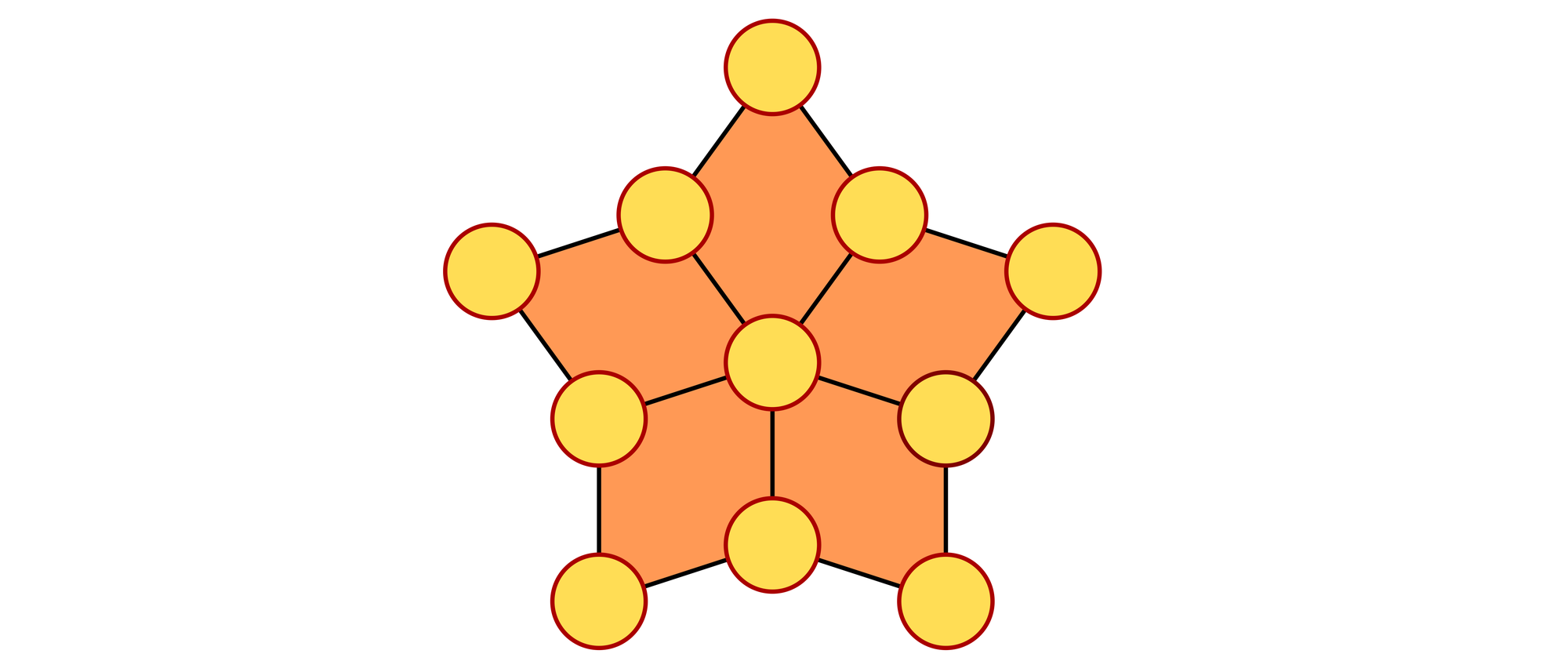
Die heutige Aufgabe geht auf eine Idee von John Kruse aus Aachen zurück. Setzen Sie in die elf Kreise des Sterns elf verschiedene Primzahlen, so dass bei jedem Rhombus die Summe der vier Zahlen auf seinen Ecken 51 ergibt.
Die Summe von vier Primzahlen kann nur dann ungerade sein, wenn unter ihnen die Zwei ist. Da die elf Primzahlen verschieden sind, muss die Zwei auf dem allen Rhomben gemeinsamen Mittelfeld stehen. Für die drei anderen Primzahlen auf den Ecken der Rhomben mit der Summe 51 – 2 = 49 gibt es die acht möglichen Trios (3, 5, 41), (3, 17, 29), (5, 7, 37), (5, 13, 31), (7, 11, 31), (7, 13, 29), (7, 19, 23) und (13, 17, 19). Die Zahlen, die auf den Spitzen des Sterns stehen, gehören nur zu jeweils einem Rhombus und dürfen deshalb auch nur in einem Trio des Sterns vorkommen. Die beiden anderen Zahlen hingegen gehören zu jeweils zwei Rhomben und müssen darum in genau zwei Trios des Sterns auftreten. Es müssen folglich drei Trios so von der Liste gestrichen werden, dass nur noch zehn Zahlen vorkommen, davon fünf Zahlen einmal und fünf Zahlen zweimal. Von den vier Trios mit einer Sieben können also mindestens zwei nicht im Stern auftreten, und von den drei Trios mit einer Fünf und den drei Trios mit einer Dreizehn kann jeweils mindestens ein Trio nicht vorkommen. Durch systematisches Probieren findet man, dass man die drei Trios (5, 13, 31), (7, 11, 31) und (7, 13, 29) streichen muss. Setzt man ein beliebiges verbleibendes Trio auf einen Rhombus, ergibt sich daraus der Rest eindeutig. Abgesehen von Drehungen und Spiegelungen des Musters gibt es nur eine einzige Lösung.
Schreiben Sie uns!
Beitrag schreiben