Hemmes mathematische Rätsel: Wie stehen die Radien der beiden Kreise zueinander?
© Heinrich Hemme (Ausschnitt)
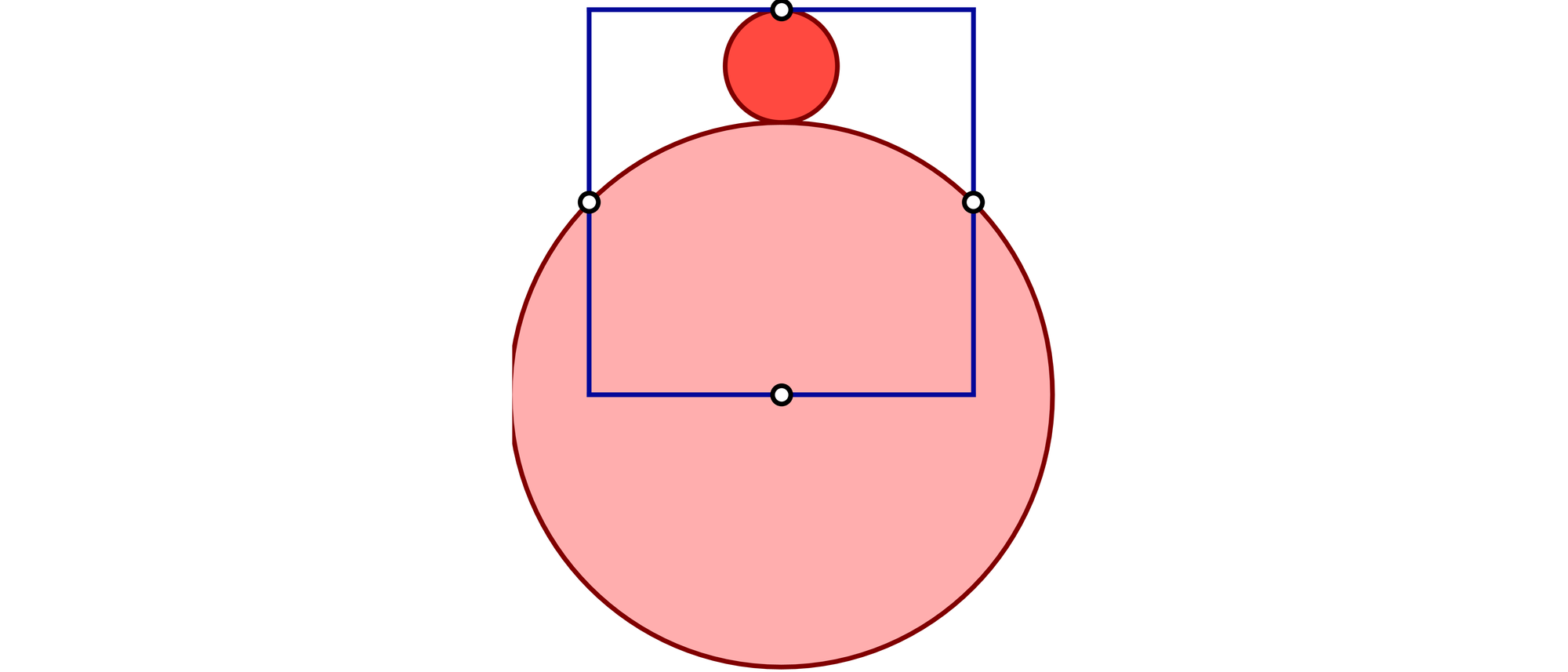
Ein kleiner Kreis und ein großer Kreis liegen so übereinander, wie es das Bild zeigt. Ein Quadrat schneidet die beiden Kreise. Drei seiner Seitenmittelpunkte liegen auf den Umfängen der beiden Kreise. Der vierte Seitenmittelpunkt fällt mit dem Mittelpunkt des großen Kreises zusammen. In welchem Verhältnis steht der Radius des kleinen Kreises zu dem des großen Kreises?
Wir bezeichnen den Radius des kleinen Kreises mit r und den des großen mit R. Die Seitenmittelpunkte des blauen Quadrats sind die Ecken eines kleineren grünen Quadrats mit der Seitenlänge R und der Diagonalenlänge 2r + R. Nach dem Satz des Pythagoras gilt R√2 = 2r + R, was sich zu r/R = 1/2(√2 – 1) ≈ 0,2071 umformen lässt.
© Heinrich Hemme (Ausschnitt)
Schreiben Sie uns!
2 Beiträge anzeigen