Hemmes mathematische Rätsel: Wie teilen Sie das Quadrat in zwei deckungsgleiche Hälften?
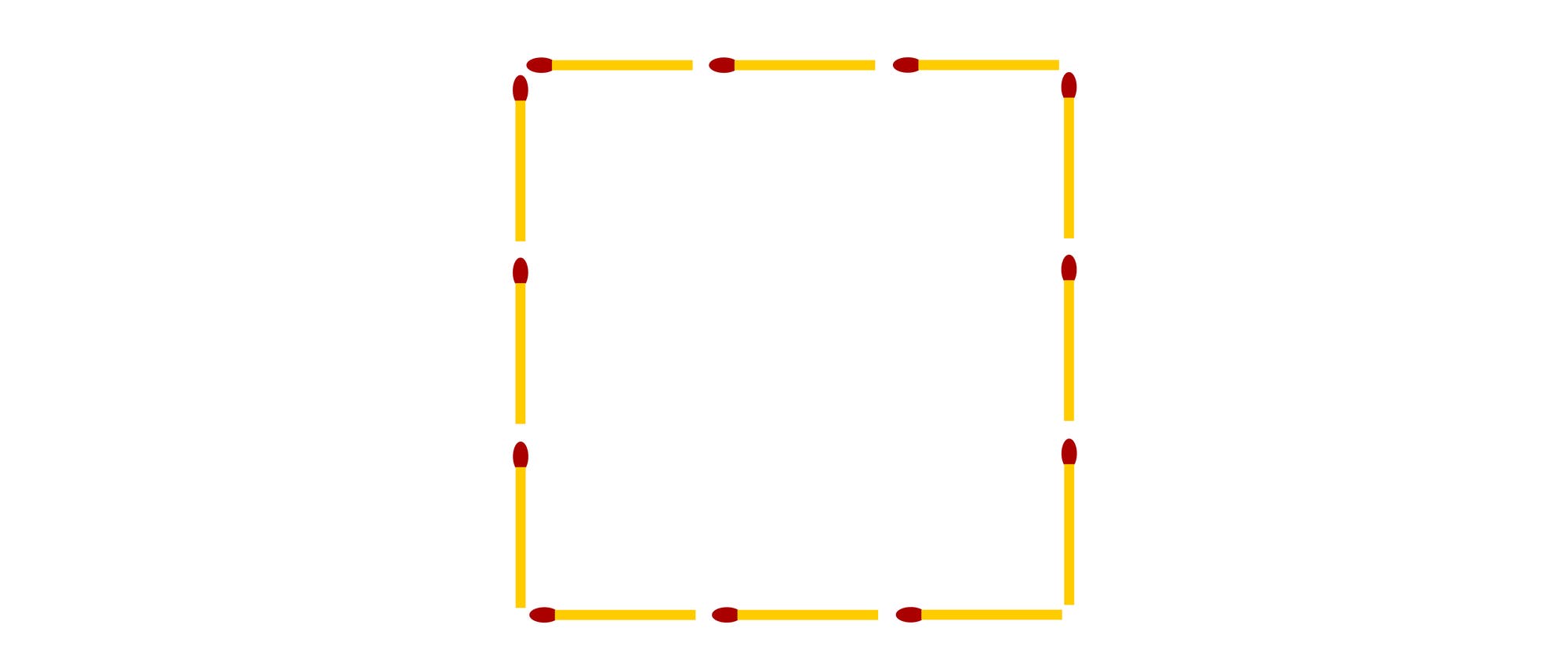
Teilen Sie das Quadrat durch vier zusätzliche Streichhölzer in zwei deckungsgleiche Hälften. Beide Enden jedes Streichholzes müssen die Enden anderer Streichhölzer berühren. Wie viele verschiedene Lösungen gibt es, wenn Muster, die sich nur durch Drehungen oder Spiegelungen unterscheiden, nicht mitgezählt werden?
Der Einfachheit halber nehmen wir an, dass alle Streichhölzer eine Länge von 1 haben. Die Diagonale des Quadrates ist 3√2 ≈ 4,24 lang und damit länger als vier Streichhölzer. Somit kommt als Startpunkt der Teilungslinie nur einer der Streichholzendpunkte auf den Seiten des Quadrates infrage. Wegen der Symmetrie sind diese alle gleichwertig. Damit die beiden Teile deckungsgleich werden, muss die Teilungslinie durch den Mittelpunkt des Quadrates laufen und die eine Hälfte der Linie die um 180° um den Mittelpunkt des Quadrates gedrehte andere Hälfte sein. Dadurch kann sie nur die beiden folgenden Formen haben:
Die vier gleichschenkligen Dreiecke AEM, MFB, AGM und MHB sind deckungsgleich. Die Länge der Strecke AB kann man mit dem Satz des Pythagoras zu √(12 + 32) = √10 berechnen. Somit sind die Grundlinien AM und MB genau ½√10 lang. Für den der Grundlinie gegenüberliegenden Winkel γ ergibt sich mit dem Kosinussatz somit (½√10)2 = 12 + 12 – 2 · 1 ·1 · cos γ, was man zu γ = arccos(– ¼) ≈ 104,48° umformen kann. Somit sind die anderen Winkel der Dreiecke etwa (180° – 104,48°)/2 = 37,76° groß.
Schreiben Sie uns!
Beitrag schreiben