Hemmes mathematische Rätsel: Wie viel Fläche des Viertelkreises wird abgedeckt?
Der United Kingdom Mathematics Trust (UKMT) ist eine Organisation, die die Mathematikausbildung britischer Kinder unterstützt. Der UKMT wurde 1996 gegründet und organisiert eine Reihe von Mathematikwettbewerben. Einige davon sind die »Junior Mathematical Challenge«, die »Intermediate Mathematical Challenge«, die »Senior Mathematical Challenge«, der Känguru-Wettbewerb und die »British Mathematical Olympiad«. Die meisten dieser Wettbewerbe gab es schon vor 1996, aber durch den UKMT wurde es möglich, sie zentral zu organisieren. Die heutige Kopfnuss stellte der UKMT im Jahr 2018.
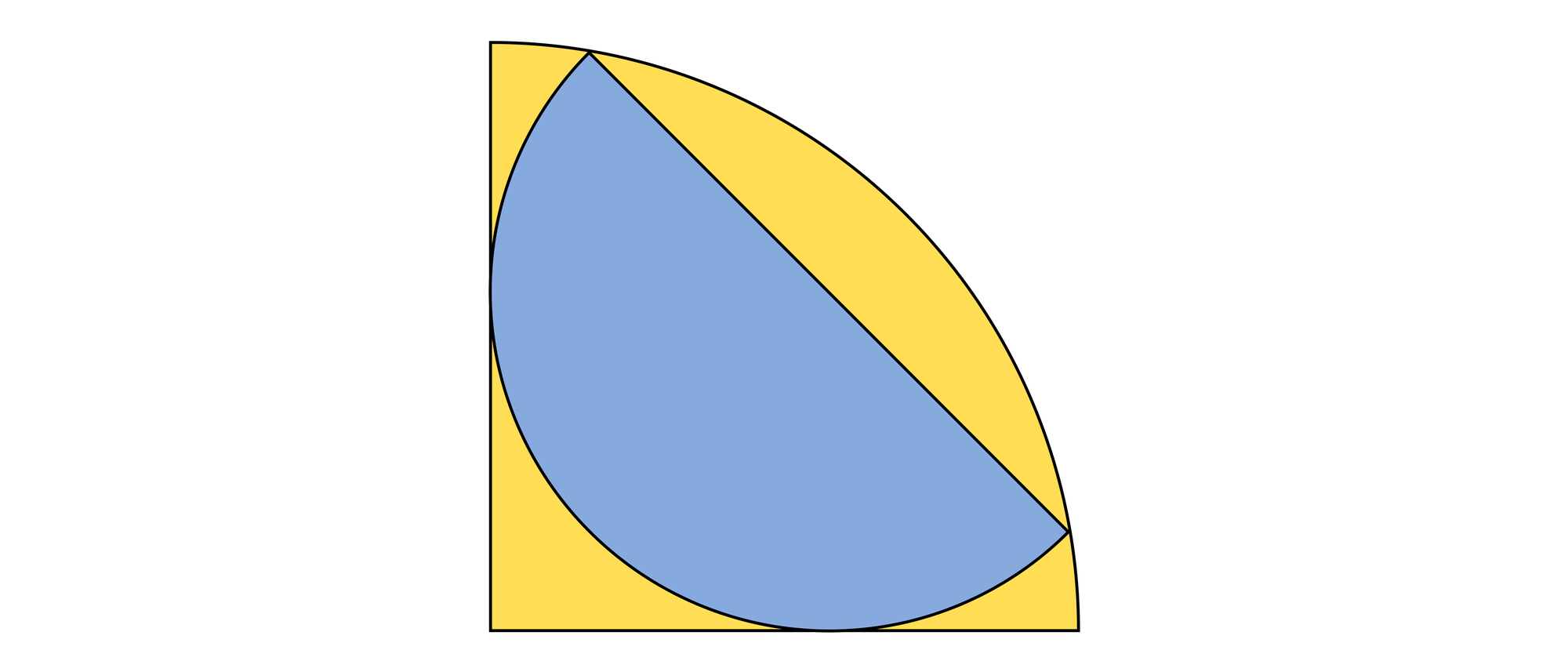
In einem Viertelkreis liegt ein Halbkreis. Seine beiden Ecken liegen auf dem Bogen des Viertelkreises, und sein Bogen berührt beide Radien des Viertelkreises. Den wievielten Teil der Viertelkreisfläche deckt der Halbkreis ab?
Der Viertelkreis hat den Mittelpunkt A und den Radius R und der Halbkreis den Mittelpunkt C und den Radius r. Die Punkte B und D sind zwei der vier Punkte, an denen sich der Viertel- und der Halbkreis berühren. Das Dreieck ABC ist rechtwinklig, und seine beiden Katheten haben die Länge r. Folglich ist seine Hypotenuse r√2 lang. Auch das Dreieck ACD ist rechtwinklig. Seine Katheten haben die Längen AC = r√2 und CD = r, und seine Hypotenuse hat die Länge R. Nach dem Satz des Pythagoras gilt R2 = (r√2)2 + r2 = 3r2. Der Viertelkreis hat den Flächeninhalt 1/4πR2 = 3/4πr2 und der Halbkreis 1/2πr2. Somit deckt der Halbkreis 1/2πr2 / (3/4πr2) = 2/3 der Viertelkreisfläche ab.
Schreiben Sie uns!
Beitrag schreiben