Hemmes mathematische Rätsel: Wie viele Abschnitte muss der Linienzug durch das Schachbrett haben?
Aus dem 2016 erschienenen Buch »Puzzle Box, Volume 1« der ukrainischen Rätselerfinder Peter und Serhiy Grabarchuk stammt die folgende kleine Kopfnuss.
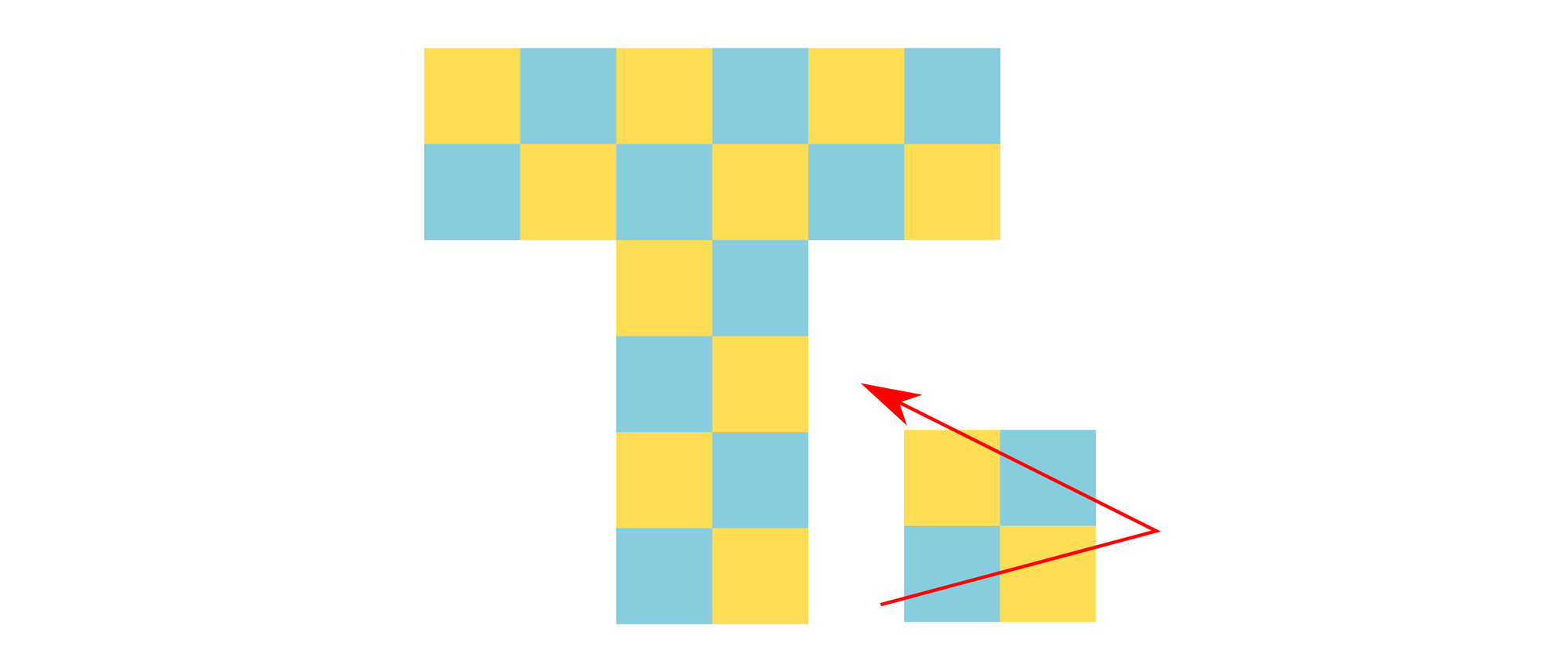
Zeichnen Sie einen Linienzug durch das T-förmige Schachbrett. Der Linienzug soll aus möglichst wenigen geraden Abschnitten bestehen. Er soll jedes Feld des Bretts genau einmal schneiden und immer abwechselnd durch ein blaues und ein gelbes Feld laufen. Ein Feld gilt als geschnitten, wenn der Linienzug zwei seiner Seiten kreuzt. Der Linienzug darf nicht durch Ecken der Felder laufen, und seine Knickstellen müssen außerhalb des Bretts liegen. Wie viele Abschnitte muss der Linienzug mindestens haben? Bei einem 2×2-feldigen Brett könnte der Linienzug beispielsweise so aussehen, wie es das kleine Bild zeigt.
Es reichen vier gerade Abschnitte für den Linienzug aus, um alle Felder des T-förmigen Schachbretts nach den Regeln aus der Aufgabe zu schneiden.
Schreiben Sie uns!
Beitrag schreiben