Hemmes mathematische Rätsel: Wie viele Alternativen gibt es?
© Heinrich Hemme (Ausschnitt)
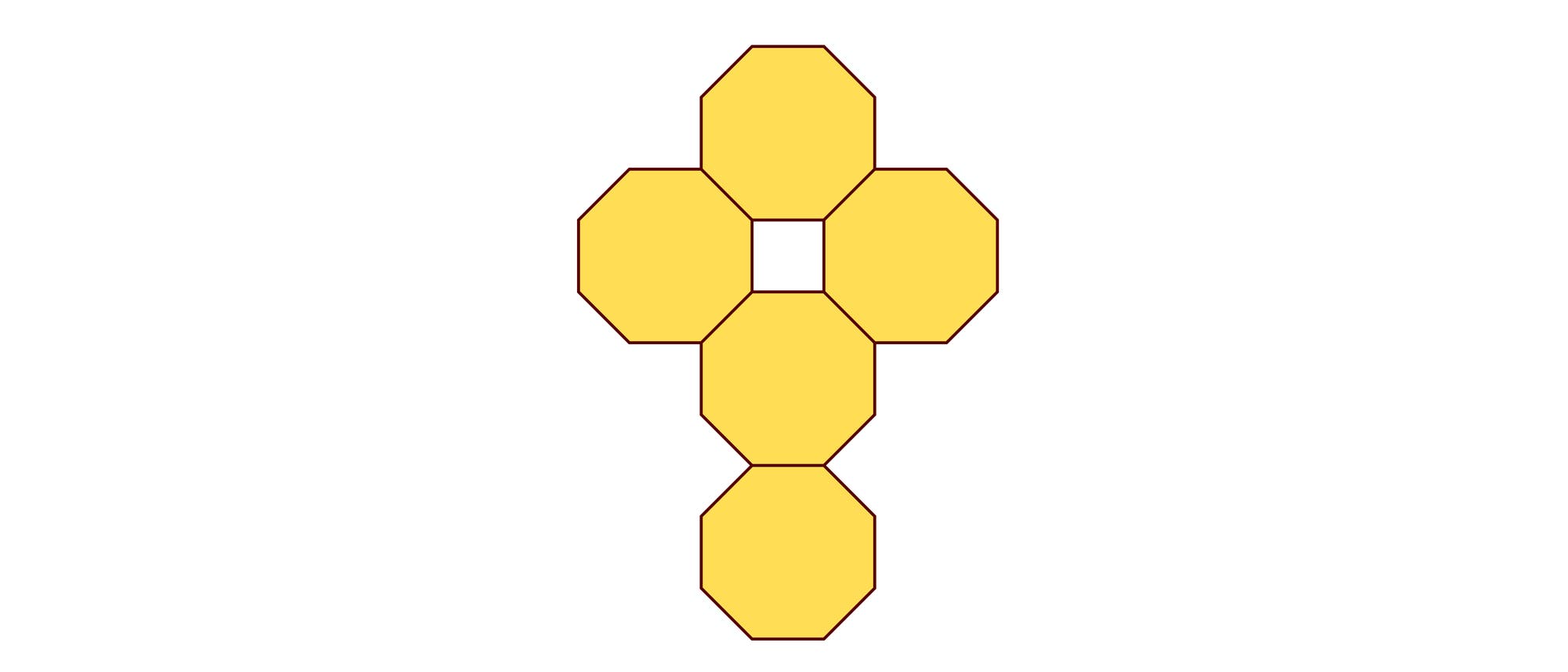
Färben Sie mit drei Farben die fünf Achtecke so, dass nirgendwo zwei gleichfarbige Achtecke eine gemeinsame Seite haben. Wie viele Möglichkeiten gibt es hierfür?
Für die Färbung des Achtecks A gibt es drei Möglichkeiten, und für die Färbung von B bleiben dann noch zwei Möglichkeiten. Werden C und D gleich gefärbt, gibt es hierfür zwei Möglichkeiten, und für E bleiben dann auch wieder zwei Möglichkeiten. Zusammen ergeben sich 3 · 2 · 2 · 2 = 24 Möglichkeiten. Werden hingegen C und D unterschiedlich gefärbt, stehen zwar für C zwei Farben zur Wahl, aber die Farben von D und E liegen dann eindeutig fest. Somit gibt es hierfür nur 3 · 2 · 2 = 12 Möglichkeiten. Insgesamt können die Achtecke also auf 36 verschiedene Weisen gefärbt werden.
© Heinrich Hemme (Ausschnitt)
Schreiben Sie uns!
Beitrag schreiben