Der deutsche Physiker und Elektrotechniker Ferdinand Braun wurde 1850 in Fulda geboren und starb 1918 in New York. Zwei seiner zahlreichen Erfindungen sind die Halbleiterdiode, die auch heute noch in jedem elektronischen Gerät verwendet wird, und die Braunsche Röhre, die im 20. Jahrhundert als Bildröhre in allen Fernsehern steckte. Für seine Arbeiten über die drahtlose Telegrafie erhielt er 1909 den Nobelpreis für Physik. Braun galt bei seinen Studenten als Meister des verständlichen Vortrags. 1876 veröffentlichte er das Buch »Der junge Mathematiker und Naturforscher«, das den Untertitel »Lehrreiches und Wissenswerthes zur Unterhaltung für Jung und Alt« trägt. Darin stellt er seinen Leserinnen und Lesern das folgende Streichholzrätsel.

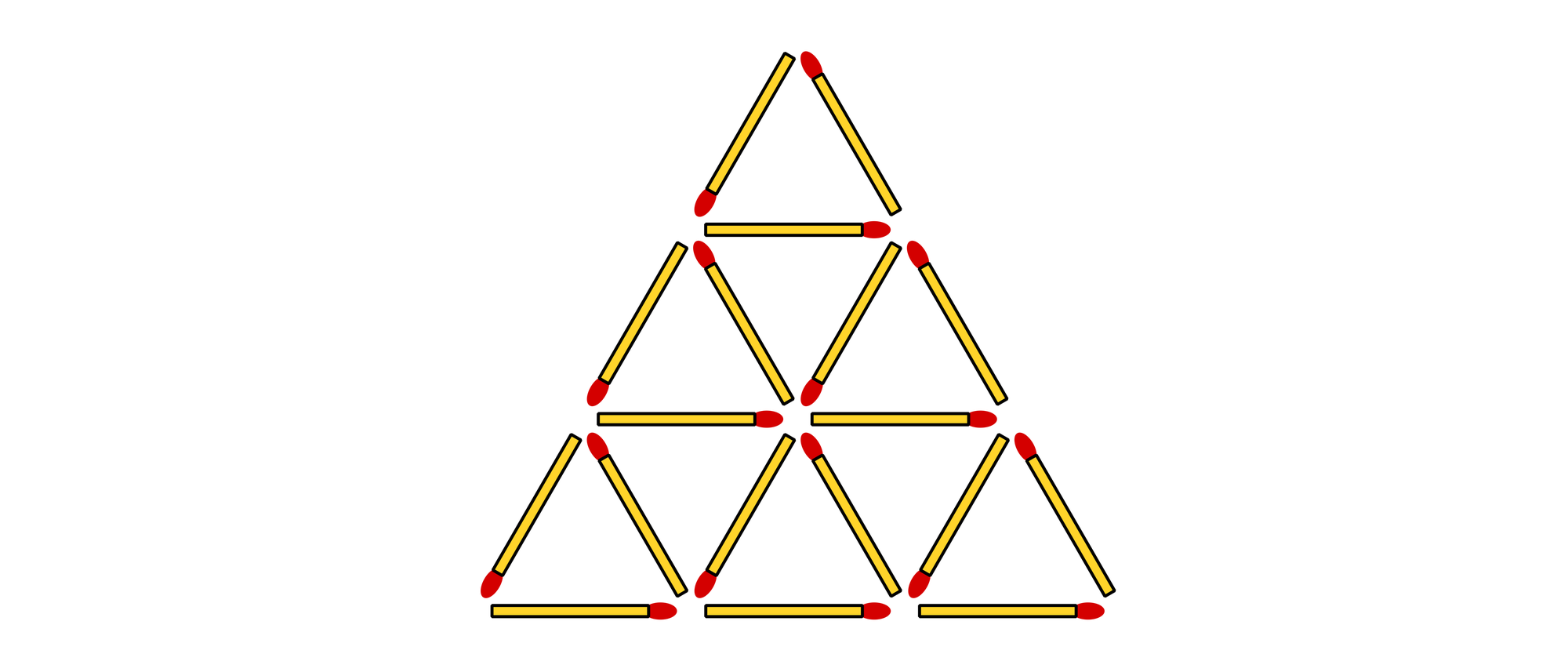
18 Streichhölzer sind zu dem abgebildeten Muster angeordnet worden. Es besteht aus neun Dreiecken von einem Holz Seitenlänge, drei Dreiecken von zwei und einem Dreieck von drei Hölzern Seitenlänge. Entfernen Sie fünf Streichhölzer, so dass die restlichen Hölzer nur noch insgesamt fünf Dreiecke bilden. Dabei muss jedes Streichholz eine Seite oder Teil einer Seite von mindestens einem Dreieck sein.

Braun deutet in seinem Buch an, dass das Problem mehrere Lösungen haben könnte, gibt aber im Lösungsteil kommentarlos nur eine einzige Lösung an. Wie viele verschiedene Lösungen finden Sie?