Hemmes mathematische Rätsel: Wie viele Münzen dürfen entfernt werden?
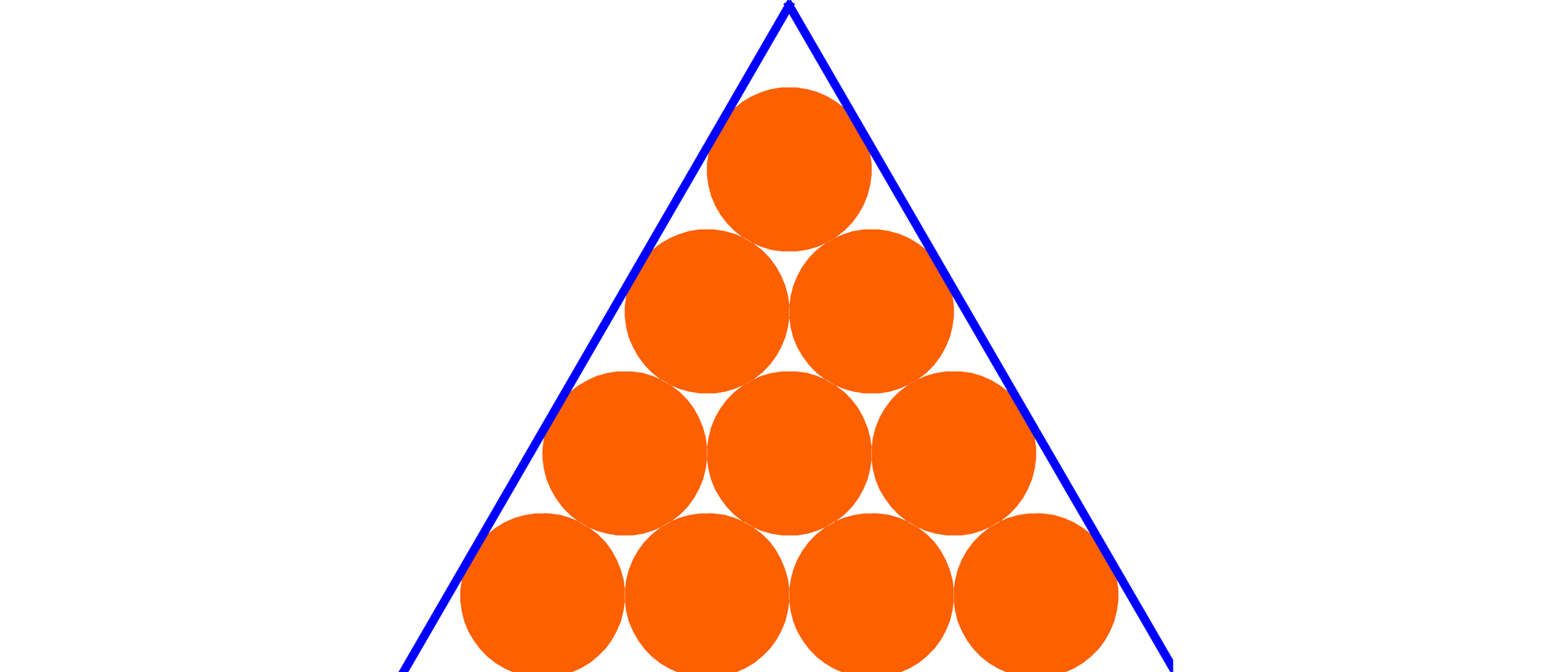
Zehn 1-Euro-Münzen liegen in einem dreieckigen Rahmen, der so klein ist, dass sich keine Münze auch nur einen Millimeter verschieben lässt. Wie viele Münzen kann man höchstens aus dem Rahmen entfernen, ohne dass sich nun eine der restlichen Münzen verschieben lässt?
Es darf kein Paar sich berührender Münzen aus dem Rahmen genommen werden, denn sonst ließe sich eine Münze, die dieses Paar berührt hat, in die Lücke schieben, die es hinterlassen hat. Die drei Eckmünzen und die Münze in der Mitte lassen sich hingegen entfernen, ohne dass die restlichen sechs Münzen sich anschließend verschieben lassen.
Würde man eine andere Münze als eine dieser vier Münzen entfernen, müsste sie eine der sechs Randmünzen sein. Diese sind wegen der Symmetrie alle gleichwertig, deswegen nehmen wir die gelbe Münze fort. Von den vier roten Münzen kann man nun keine mehr fortnehmen, denn sie berühren alle die gelbe Münze. Von den zwei blauen und den drei grünen Münzen darf man jeweils nur eine Münze entfernen. Dadurch kommt man auf insgesamt drei entfernte Münzen. Die drei Eckmünzen und die Mittelmünze bilden also tatsächlich das Maximum.
Schreiben Sie uns!
5 Beiträge anzeigen