Hemmes mathematische Rätsel: Wie viele Vierecke kann man auf dem Geobrett mit einem Gummi bilden?
Caleb Gattegno (1911–1988) war, obwohl er selbst nie eine formale Ausbildung genossen hatte, einer der einflussreichsten und produktivsten Mathematikpädagogen des 20. Jahrhunderts. Er erfand die Geobretter und machte sie populär.
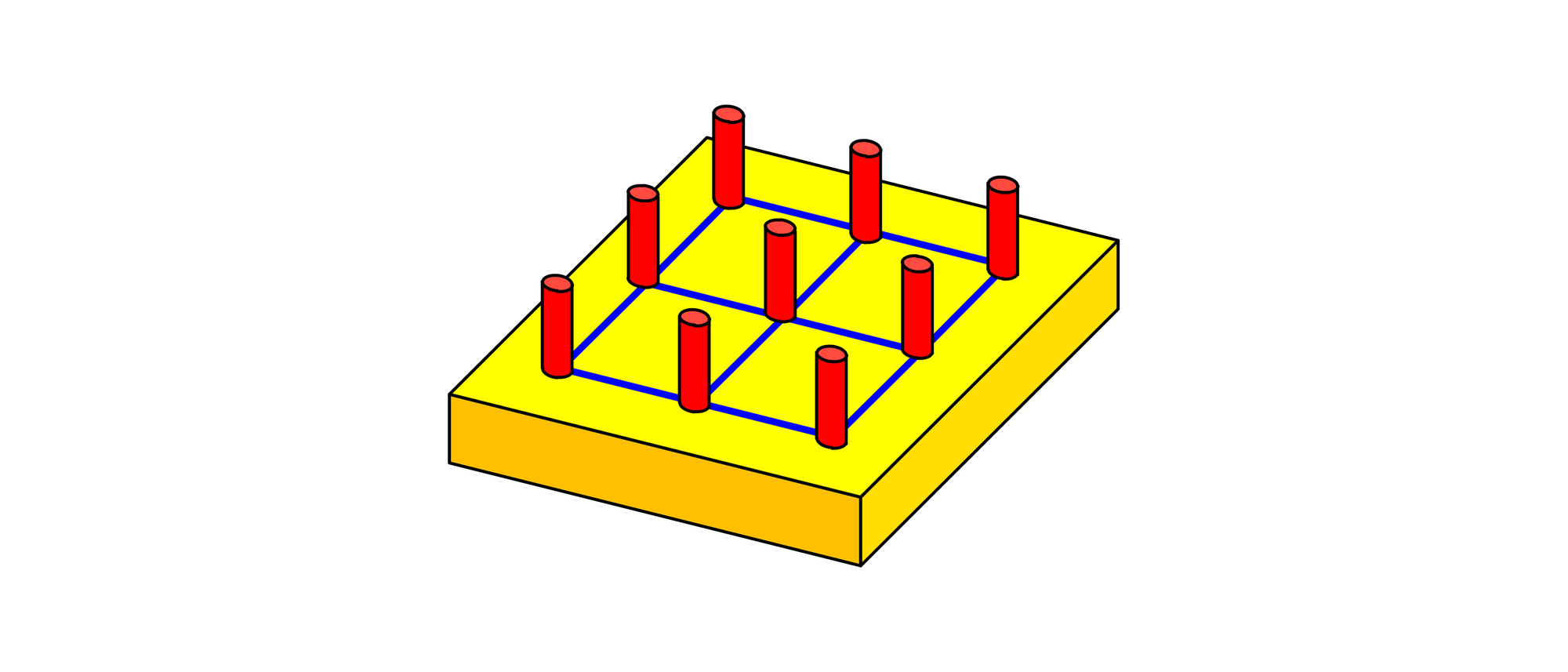
Wie viele verschiedene Vierecke lassen sich mit einem Gummiring auf einem Geobrett mit 3×3 Stiften bilden? Eines davon ist das Trapez aus der Abbildung, aber es gibt noch eine ganze Reihe anderer.
Vierecke, die durch Verschiebungen, Drehungen und Spiegelungen ineinander übergehen, zählen nicht als verschieden. Außerdem sind überschlagene Vierecke, bei denen sich der Gummiring selbst schneidet, und entartete Vierecke, die Innenwinkel von 0° oder 180° besitzen, nicht erlaubt.
Durch systematisches Probieren findet man 16 verschiedene Vierecke. Vier davon sind nicht konvex. Die Aufgabe und auch die Lösungen stammen aus dem 2005 in New York erschienenen Buch »Knotty Number Problems & Other Puzzles« des 1924 in Novi Sad geborenen Spiele- und Rätselerfinders Ivan Moscovich.
Schreiben Sie uns!
Beitrag schreiben