Hemmes mathematische Rätsel: Wie viele Zeilen und Spalten werden gesucht?
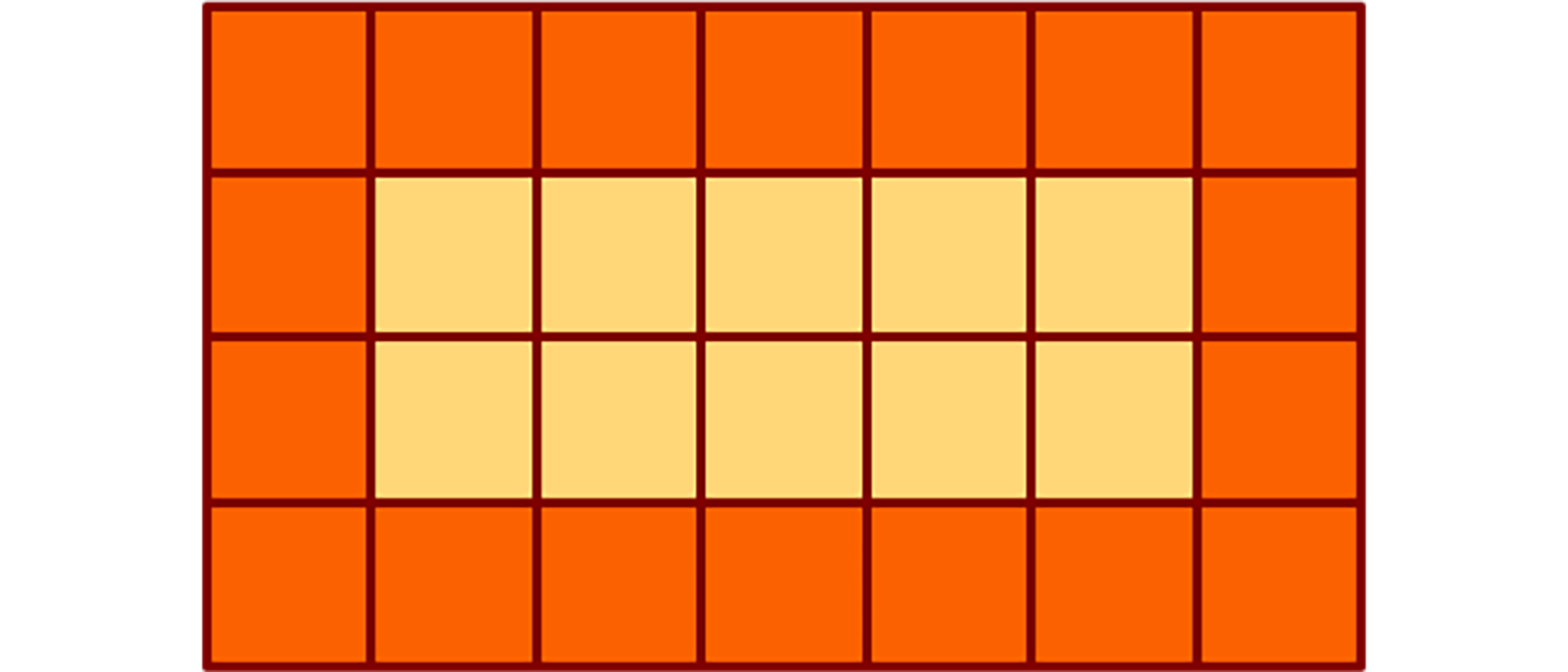
Ein 4×7-feldiges Schachbrett hat 10 Innenfelder und 18 Randfelder. Wie viele Zeilen und wie viele Spalten muss ein Schachbrett haben, damit es genauso viele Innen- wie Randfelder besitzt?
Ein m×n-feldiges Schachbrett hat insgesamt mn Felder, wovon (m – 2)(n – 2) Felder Innenfelder sind. Wenn es genauso viele Randfelder gibt, gilt 2(m – 2)(n – 2) = mn. Löst man die Gleichung nach m auf, erhält man m = 4 ∙ (n – 2)/(n – 4). Die Differenz zwischen Zähler und Nenner in dem Bruch beträgt 2. Für gerade Werte von n lässt er sich darum nur durch 2 und für ungerade Werte gar nicht kürzen. Da die rechte Seite der Gleichung eine natürliche Zahl ergeben muss, kann der Nenner n – 4 nur 1, 2, 4 oder 8 sein, und damit n nur 5, 6, 8 oder 12. Dies ergibt m = 12, 8, 6 oder 5. Wenn man m ≤ n annimmt, gibt es als Lösungen nur das 5×12- und das 6×8-feldige Schachbrett.
Schreiben Sie uns!
3 Beiträge anzeigen