Winkelbetrug
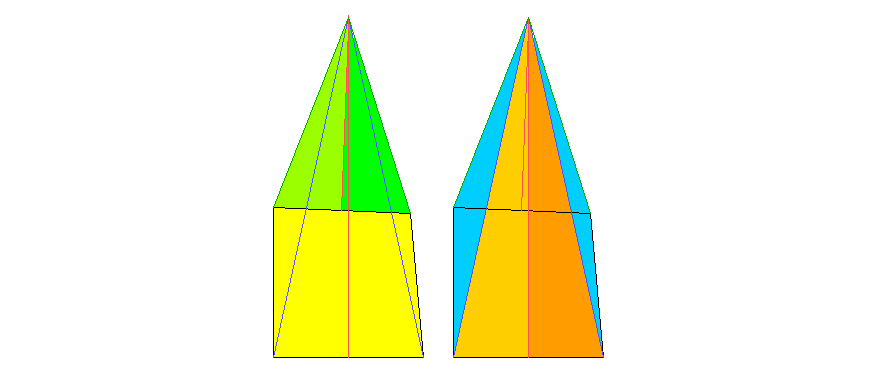
Das gelbe Viereck hat links, unten und rechts drei (schwarze) gleich lange Seiten, links unten einen rechten Winkel und rechts unten einen etwas kleineren (85o). Wir wollen nun zeigen, dass die beiden unteren (spitzen) Winkel der blauen Dreiecke gleich groß sind. Dazu konstruieren wir die folgende Figur:
1. Wir errichten zur unteren und zur oberen Seite die Mittellote.
2. Wir verbinden deren Schnittpunkt (ganz oben) mit allen vier Ecken des gelben Vierecks.
Aus den beiden gleichschenkligen Dreiecken (erstes Dreieck: beide grünen Seiten ("Außenseiten" der grünen Dreiecke) und die obere schwarze Seite, zweites Dreieck: beide blauen Seiten ("Innenseiten" der blauen Dreiecke) und die untere schwarze Seite) findet man, dass die zwei blauen schlanken Dreiecke (in der rechten Zeichnung) links und rechts deckungsgleich sind.
Was stimmt an dieser Konstruktion oder Aussage nicht? Finden Sie den Fehler.
Zeichnen Sie das Bild etwas realistischer, vielleicht auch mit weniger als 85o.
Das linke Bild ist korrekt gezeichnet, die anderen beiden sind Wiederholungen des geschummelten Bildes aus der Frage. Bei dem Winkel 85o liegt der wirkliche Schnittpunkt der Lote weit über Ihrem Bildschirm. Die beiden blauen Dreiecke sind tatsächlich kongruent (deckungsgleich), aber ohne Klappung. Das heißt, ihre unteren spitzen Winkel liegen nicht beiderseits auf der Innenseite der Vierecks-Winkel.
Die Aufgabe ist ein Klassiker der bewussten Irreführungen. Tatsächlich werden in der euklidischen (im Gegensatz zur analytischen) Geometrie Vorzeichen von Strecken oder Winkeln nicht konsequent formalisiert, und leichtsinnigerweise entnimmt man dann meistens unkritisch den Skizzen, ob man addieren oder subtrahieren soll.
Schreiben Sie uns!
Beitrag schreiben