Hemmes mathematische Rätsel: Zahlenquadrat aus Rom
Diese Aufgabe habe ich 2010 erdacht, und der Wiener Mathematiker Helmut Postl war der erste, der sie gelöst hat.
Setzen in jedes Feld eines N×N-feldigen Quadrats ein römisches Zahlenzeichen, so dass jede Zeile und jede Spalte eine gültige römische Zahl bildet. Die 2N Zahlen müssen alle verschieden sein. Natürlich werden die Zeilen von links nach rechts und die Spalten von oben nach unten gelesen. Wie groß kann N höchstens sein?
Es dürfen nur die Zeichen I, V, X, L, C, D und M verwendet werden, und es muss die normale Subtraktionsregel benutzt werden. In einer römischen Zahl werden die Ziffern von links nach rechts nach absteigenden Werten geordnet. Das heißt, normalerweise steht links von einer Ziffer keine kleinere Ziffer. Die Subtraktionsregel in ihrer Normalform besagt, dass die Ziffern I, X und C einem ihrer nächst oder übernächst größeren Zahlzeichen vorangestellt werden dürfen und dann in ihrem Zahlwert von dessen Wert abzuziehen sind. Nur vom M dürfen mehr als drei Zeichen aufeinander folgen. Beispielweise ist 5000 = MMMMM.
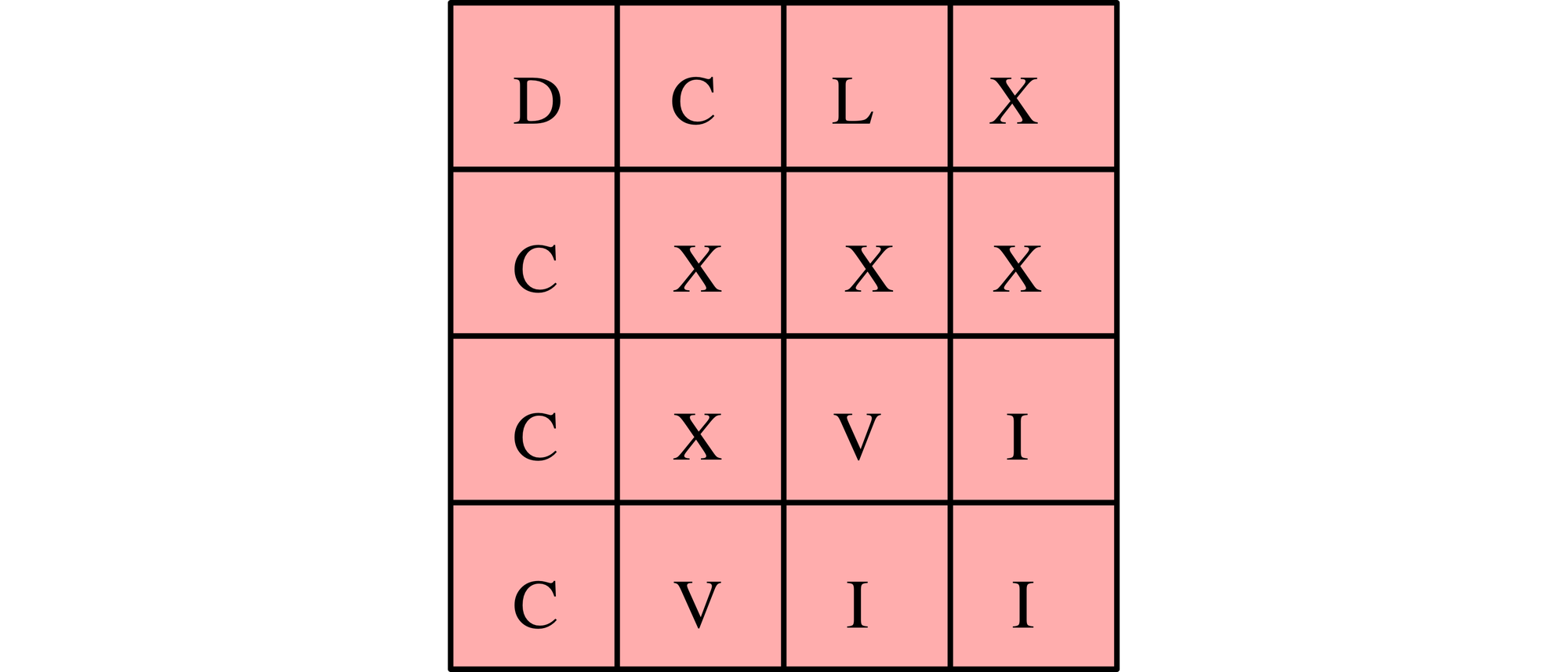
Das Abbildung zeigt ein Beispiel für N = 4. Die Zeilen und Spalten enthalten die Zahlen DCLX, CXXX, CXVI, CVII, DCCC, CXXV, LXVI und XXII, die alle verschieden sind. Dies ist allerdings nicht der größtmögliche Wert für N.
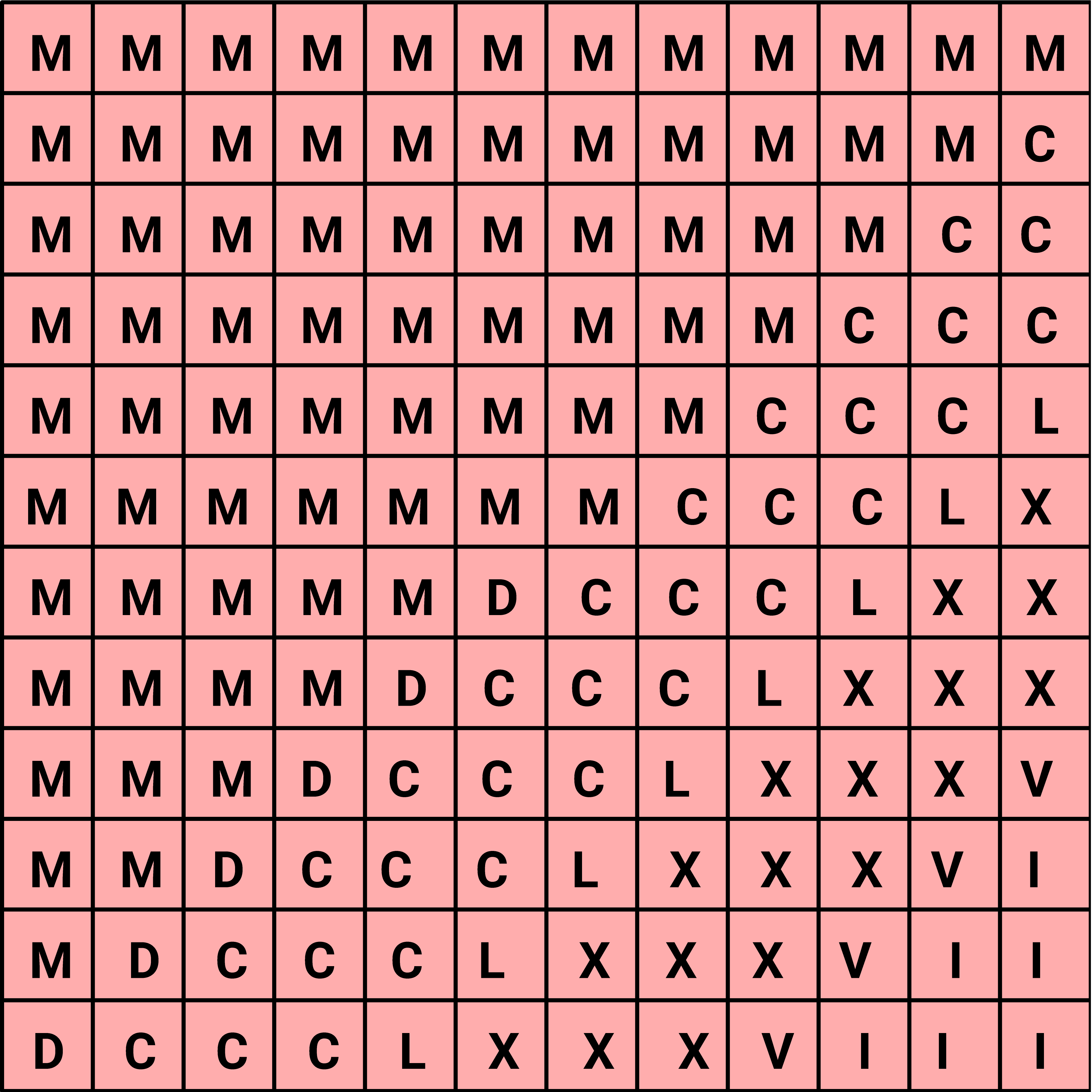
Die längste römische Zahl, die kein M enthält, ist DCCCLXXXVIII und zwölf Zeichen lang. Alle längeren Zahlen beginnen mit einem M. Darum enthalten ab N = 13 die erste Zeile und die erste Spalte des Rasters ausschließlich M und stellen somit zwei gleiche Zahlen dar. Folglich kann es keine Lösungen des Problems für N > 12 geben. Für N = 12 gibt es allerdings Lösungen. Das Bild zeigt eine von ihnen. Auf jeder Diagonalen des Rasters, die von oben rechts nach unten links verlaufen, stehen nur gleiche Zahlenzeichen. Die einzige Ausnahme ist die mittlere Diagonale, die sechs M und sechs D enthält.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.