Der Mathematische Monatskalender: Eugenio Beltrami, vom Sekretär zum Mathematiker

Als Eugenio Beltrami geboren wurde, gehörte die Lombardei und Beltramis Heimatstadt Cremona noch zum habsburgischen Kaiserreich. Seine Eltern, Giovanni Beltrami und die Venezianerin Elisa Barozzi, stammten aus angesehenen Künstlerfamilien; Eugenios Vater verdiente den Lebensunterhalt durch den Verkauf von Miniaturen. Nach dem schulischen Abschluss im Jahr 1853 schrieb sich Eugenio als Student an der Mathematischen Fakultät der 70 Kilometer entfernten Universität von Pavia ein.
Dank hervorragender Ergebnisse im Aufnahmetest kam er in den Genuss eines Stipendiums und konnte in einem Internat, dem Collegio Ghislieri, wohnen. Aber bereits im folgenden Jahr wurde er – zusammen mit fünf anderen Stipendiaten – wegen angeblicher Anzettelung von Unruhen vom Collegio verwiesen. Diese unangemessen hohe Strafe hatte für den begabten Studenten verheerende Auswirkungen: Da seine Familie die finanziellen Mittel nicht aufbringen konnte, musste Eugenio Beltrami Ende 1856 sein bis dahin sehr erfolgreich verlaufendes Studium abbrechen und in Verona eine Beschäftigung als gering bezahlter Sekretär eines Eisenbahn-Ingenieurs der Provinz Lombardei-Venetien annehmen.
Doch bereits nach drei Monaten kündigte ihm der Generaldirektor der Bahn aus politischen Gründen. Dies blieb jedoch ohne Folgen, da sich zur selben Zeit die politischen Verhältnisse radikal veränderten: Im Rahmen des italienischen Unabhängigkeitskriegs (Risorgimento) fiel die gesamte Lombardei an das Königreich Piemont-Sardinien. Beltrami behielt seine Stelle beim Eisenbahn-Ingenieur und folgte diesem nach Mailand. Dort fand er wieder Zeit, sich mit Mathematik zu beschäftigen; erste Beiträge wurden von der Fachzeitschrift »Annali di Matematica« angenommen.
Der mathematische Monatskalender
Ihre wissenschaftlichen Leistungen sind weit verbreitet, doch wer waren die Mathematik-Genies, die unser Verständnis der Welt nachhaltig prägten? Seine ersten »mathematischen Monatskalender« hatte Heinz Klaus Strick, ehemaliger Leiter des Landrat-Lucas-Gymnasiums in Leverkusen-Opladen, für seine Schülerinnen und Schüler geschrieben, ergänzt durch passende Briefmarken der vorgestellten Personen. Alle spannenden Lebensläufe, skurrilen Porträts und unglaublichen Geschichten hinter den namhaften Persönlichkeiten finden Sie hier.
In der Zwischenzeit wurde Francesco Brioschi, Beltramis ehemaliger Mathematikprofessor aus Pavia, von Camillo Benso, dem Anführer der Unabhängigkeitsbewegung, in eine Kommission berufen, die eine Unterrichtsreform für das zukünftige vereinigte Italien vorbereiten sollte (unter anderem gehörte auch Giuseppe Verdi diesem Gremium an). In seiner Zuständigkeit als Staatssekretär nutzte Brioschi 1862 die Möglichkeit, Beltrami auch ohne formale Abschlüsse auf eine Stelle als Professore straordinario für Algebra und Analytische Geometrie an der Universität Bologna zu berufen.
Nach diesem Schritt waren alle akademischen Ämter für Beltrami offen: 1863 nahm er das Angebot von Enrico Betti an, dem Rektor der Universität Pisa, eine Professur für Geodäsie zu übernehmen. 1866 kehrte er als Professor für Rationale Mechanik nach Bologna zurück. (Als rationale Mechanik bezeichnet man den Ansatz, Gesetzmäßigkeiten der Mechanik auf streng logischem Weg herzuleiten; dabei geht man – ähnlich wie in der Geometrie – von bestimmten Hypothesen (Axiomen) aus, die durch Experimente begründet sind.)
Eine neue Art der Geometrie
Durch Francesco Brioschi und Enrico Betti war Beltrami mit einem Teilbereich der Mathematik in Berührung gekommen, der ihn in den nächsten Jahren besonders beschäftigen sollte: die nichteuklidische Geometrie. Brioschi und Betti hatten 1858 Göttingen besucht und vor Ort die Ideen Bernhard Riemanns zur Geometrie kennen gelernt; nach ihrer Rückkehr übersetzten sie seine Arbeiten und hielten Vorlesungen über seine Ansätze.
1868 veröffentlichte Beltrami zwei Beiträge in den »Annali di Matematica«, die internationales Aufsehen erregten: »Saggio d'interpretazione della geometria non-euclidea« (Aufsatz über die Interpretation der nichteuklidischen Geometrie) und »Teoria fondamentale degli spazii di curvatura costante« (Grundlegende Theorie der Räume mit konstanter Krümmung).
Seit Jahrhunderten hatten Mathematiker sich mit dem Parallelenaxiom von Euklid auseinandergesetzt und untersucht, ob dies nicht durch ein anderes ersetzt werden könnte oder welche Konsequenzen es hätte, wenn es durch seine Negation ersetzt würde. Die größten Fortschritte hatte hierbei der Schweizer Mathematiker Johann Lambert erzielt, der 1766 unmittelbar vor der Entdeckung der hyperbolischen Geometrie stand, aber den entscheidenden Schritt nicht wagte. Carl Friedrich Gauß, von dem die Bezeichnung »nichteuklidisch« stammt, entdeckte um 1817, dass eine Winkelsumme im Dreieck von weniger als 180° zu einer merkwürdigen, aber völlig konsistenten Geometrie führt. Da er befürchtete, dass durch eine Veröffentlichung sein Ruf beschädigt werden könnte, behielt er die Erkenntnisse für sich.
Auch János Bòlyai, der Sohn von Gauß' Freund Farkas, kam zu gleichen Einsichten. Doch Gauß fand nicht die anerkennenden Worte, um János zur Fortsetzung seiner Untersuchungen zu ermutigen. Selbst die Veröffentlichungen von Nikolai Lobatschewski über eine »Imaginäre Geometrie« blieben zunächst unbeachtet.
Die Negation des Parallelenaxioms hat überraschende Konsequenzen, unter anderem:
In einem Dreieck ist die Summe der Innenwinkel stets kleiner als 180°.
Stimmen zwei Dreiecke in den Winkeln überein, dann sind sie zueinander kongruent.
Die Menge aller Punkte, die von einer gegebenen Geraden denselben positiven Abstand haben und in derselben Halbebene dieser Geraden liegen, bilden selbst keine Gerade.
Durch drei Punkte, die nicht auf einer Geraden liegen, kann man nicht immer einen Kreis zeichnen.
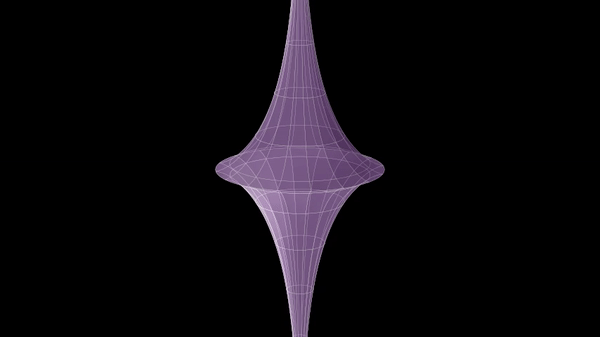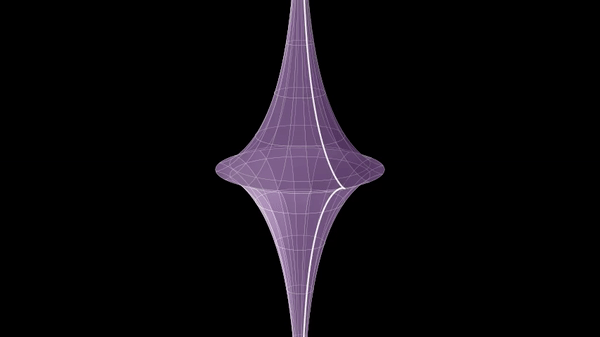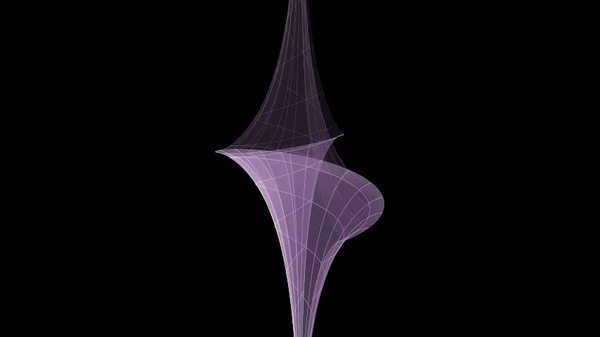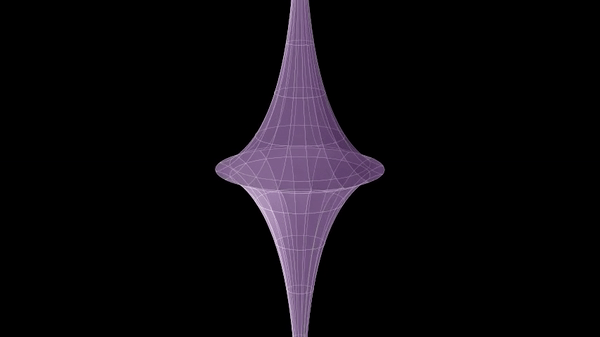
Beltrami war der Erste, der ein Modell für eine hyperbolische Geometrie angeben konnte: In seinem Saggio-Beitrag aus dem Jahr 1868 untersuchte er die Normalprojektion der Rotationsfläche einer »Traktrix« in das Innere einer Kreisfläche. Der Name der Schleppkurve stammt vom lateinischen Wort trahere (schleppen); beschrieben wird die Bewegung des Endpunkts einer Stange, die zunächst (vom Ursprung aus) auf der x-Achse liegt und deren Anfangspunkt dann längs der y-Achse gezogen wird.

Diese Fläche mit konstanter negativer Krümmung bezeichnete Beltrami als Pseudosphäre. Geodätische Linien auf der Pseudosphäre werden durch die Projektion zu Sehnen in der Kreisfläche, wobei die Endpunkte jeweils nicht dazugehören. Durch einen Punkt P der Kreisfläche gibt es unendlich viele Sehnen, die keinen gemeinsamen Punkt mit einer gegebenen Sehne g haben. Diese Eigenschaft entspricht der Negation des Parallelenaxioms: »Zu einer gegebenen Geraden g und einem nicht darauf liegenden Punkt P gibt es mehr als eine Parallele durch diesen Punkt« (hier sogar unendlich viele).
Beltrami hatte Anfang der 1860er Jahre den an Tuberkulose erkrankten Bernhard Riemann während dessen Kuraufenthalts in Norditalien persönlich kennen gelernt und sich mit ihm ausgetauscht. Nach Riemanns Tod 1866 begann dessen Freund Richard Dedekind die nachgelassenen Werke herauszugeben, darunter war auch der Text von Riemanns nicht veröffentlichtem Habilitationsvortrag aus dem Jahr 1854 (»Über die Hypothesen, welche der Geometrie zu Grunde liegen«). Beltrami, dem der Inhalt des Vortrags bis dahin nicht bekannt war, konnte daraufhin im zweiten Beitrag (»Teoria«) sein Modell verallgemeinern. Fehlende Aspekte in Beltramis Modell wurden später durch Felix Klein (1871) und David Hilbert (1901) vervollständigt.
1870 war der Einigungsprozess Italiens abgeschlossen und Rom neue Hauptstadt des Königreichs. Beltrami nahm eine Berufung der neu gegründeten Universität Rom auf einen Lehrstuhl für Rationale Mechanik an und wurde als Mitglied in die neu gegründete (staatliche) Reale Accademia dei Lincei aufgenommen. 1876 wechselte er dann auf eine Professur für Mathematische Physik an die Universität Pavia.
Dem inzwischen vielfach umworbenen Mathematiker, der seine Forschungsarbeit nunmehr auf mathematische Anwendungen verlagerte, war die wissenschaftliche Tätigkeit wichtiger als die Übernahme angesehener Ämter; schließlich gab er dennoch dem Drängen der Universität Rom nach und kehrte 1891 dorthin zurück. 1898 wurde er einstimmig zum Präsidenten der Accademia gewählt und 1899 (nach der gesetzlich vorgeschriebenen Wartezeit) auch vom italienischen König zum Mitglied des Senato del Regno (eine der Parlamentskammern) auf Lebenszeit ernannt.
Der vielfach geehrte Mathematiker (er war Mitglied der Akademien der Universitäten Bologna, Mailand, Turin, Neapel, Paris, Göttingen, Brüssel, München, Berlin und London) starb Anfang des Jahres 1900 im Alter von 64 Jahren.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.