Start
Web-Artikel
Lexikon
Vorträge
Ausbildung
Essays
Rhetorik
Links
Autor
Kontakt

Was ist Zeit?

"Zeit ist die Suche nach Vergänglichkeit."

Andreas Müller

pdf pdf

Einführung

Das Wesen der Zeit ist für unsere Wahrnehmung ein kontinuierliches Dahinfließen der Ereignisse, versinnbildlicht und messbar durch eine Sanduhr. Mit jedem fallenden Sandkorn ist mehr Zeit verstrichen. Veränderungen sind Indikatoren für das Verrinnen der Zeit. Was genau muss man unter dem Begriff Zeit verstehen?

Es zeigt sich, dass eine angemessene Beantwortung dieser Frage mit den Methoden der modernen Physik angegangen werden kann. Sie lehrt uns, dass die Zeit mehr ist als das, was wir aus der alltäglichen, beschränkten Perspektive glauben. Dabei gelangt man schnell an die Grenzen des Vorstellbaren. Zahlreiche Beobachtungen bestätigen jedoch glänzend die Richtigkeit der Relativitätstheorie und Quantentheorie. Sie gelten als bewährte Theorien, die viele Sachverhalte der unbelebten Natur beschreiben und prognostizieren können. In jüngster Zeit haben sich weitere Theorien hervorgetan, die sich erst bewähren müssen. Die daraus resultierenden Zeitbegriffe sind neu und revolutionär.
Bevor ich die Ausflüsse dieser Theorien diskutiere, möchte ich zunächst eine kleine Reise durch unterschiedliche wissenschaftliche Disziplinen unternehmen. Ich möchte kurz darstellen, wie der Zeitbegriff jeweils definiert wird und welche Rolle er in der betreffenden Disziplin spielt. Dann folgt ein kurzer Abriss über die Historie des Zeitbegriffs. Viel Raum nimmt in diesem Essay der Zeitbegriff in der Physik ein. Zum Schluss werde ich die geisteswissenschaftlichen Aspekte des physikalischen Zeitbegriffs herausarbeiten. Wesentlich ist die Bedeutung der so gewonnenen Einsicht in das Wesen der Zeit für den Menschen.

Disziplinäre Zeitbegriffe

Ich beginne mit einem unmittelbar menschlichen Aspekt. Die psychologische Zeit hängt vom subjektiven Zeiterleben des Individuums ab. Man spricht von einem Zeitgefühl und stellt fest, dass beim Warten die Zeit scheinbar langsamer vergeht, während bei einer kurzweiligen Beschäftigung die Zeit "verfliegt". Man spricht auch gerne von der "inneren Uhr". Es handelt sich um ein Zeitempfinden, das im Menschen veranlagt zu sein scheint. Ist Zeit bloß ein menschliches Konstrukt, ist sie anthropogene Zeit und hat keinen Sinn, keine Existenz, wenn man sie losgelöst vom Menschen betrachtet?
Für uns gibt es Zeit, weil wir ein Gedächtnis haben und fähig sind, uns an Vergangenes zu erinnern. Aber auch ohne den Menschen macht der Zeitbegriff Sinn. Dies macht sich bemerkbar, wenn man Objekte für sich betrachtet. Wie bereits in der Einführung vorweggenommen, sind Veränderungen Indikatoren für eine Zeit. Somit ist Zeit in direkter Relation zu Dingen zu sehen. Objekte unterliegen einer Entwicklung, die mit der Zeit voranschreitet - ob der Mensch anwesend ist oder nicht. Nüchtern betrachtet ist die Zeit ein Ordnungsparameter für die Entwicklung von Dingen. Nur die Angabe dieser Zahl genügt, um den Entwicklungszustand anzugeben.

Die biologische Zeit ist an sich ein ambivalenter Begriff: einerseits assoziiert man damit die Vergänglichkeit des Lebens. Jedes Lebewesen hat nur eine gewisse Lebensspanne zur Verfügung bzw. eine bestimmte statistische Lebenserwartung. Die Ursache dafür liegt im Altern. Im Prinzip handelt es sich dabei um einen simplen Reproduktionsvorgang des Lebewesens auf der Mikroebene: unterschiedlich organisierte Zellen (Muskelzellen, Herzzellen, Nervenzellen etc.) entstehen, erfüllen ihre Funktion und sterben ab. Sie werden zwar neu gebildet, doch ist die Kopie nicht identisch, so dass der "organisierte, lebendige Zellhaufen" sich eigentlich ständig verändert: er altert. Irgendwann ist dieses Desorganisationsprinzip so weit vorangeschritten, dass das Lebewesen eines natürlichen Todes stirbt.
Der andere Aspekt der Ambivalenz ist ein Zeitempfinden, das an den Biorhythmus koppelt. Die biologischen Zyklen wiederum koppeln an exogene Zyklen, die von der Umwelt diktiert werden. Zyklen, die von außen auf ein Lebewesen einwirken, gibt es in mannigfacher Weise. Unmittelbar ist das sicher der Tageszyklus von etwa 24 Stunden. Die Rotation unseres Planeten Erde um seine eigene Achse gibt eine Periode vor, die uns und allem irdischen Leben einen wiederkehrenden Wechsel von Tag und Nacht beschert. Hell und Dunkel, die abwechselnde Versorgung mit Strahlungsenergie der Sonne, hat natürlich einen gewichtigen Einfluss auf die Funktionsweise biologischer Systeme. Im Laufe von Äonen hat sich das Leben an diesen Zyklus angepasst. Hier muss angemerkt werden, dass der Tageszyklus über solch große Zeiträume nicht konstant ist. Die Tageslänge nimmt aufgrund der gravitativen Wechselwirkung zwischen Erde und Mond, der so genannten Gezeitenreibung, zu. Der Erdmond wirkt sich wie eine Bremse auf die Rotation der Erde aus. Dennoch fand eine Anpassung des irdischen Lebens an den Tageszyklus statt. So wandelt das Blattgrün der Pflanzen in der Photosynthese Kohlendioxid in Sauerstoff unter vitaler Einwirkung von Licht um. Die Gesamtheit irdischer Pflanzen regelt demzufolge den Gashaushalt der Erde. Dieses Phänomen wird gerne mit dem Begriff der "grünen Lunge" apostrophiert. Die Pflanzen waren erdzeitgeschichtlich die Entwicklungsvorläufer der Tiere und Menschen. So haben sich diese anderen Lebensformen an die Vorgaben der Pflanzen angepasst: Ob es nun die Atmung über Lungen, Kiemen oder Tracheen geschieht, sie beruht auf der Aufnahme des Sauerstoffs, den im Wesentlichen Pflanzen stellen.
Die periodische Lichteinwirkung der Sonne hat noch andere Konsequenzen. Der Stoffwechsel wird auch beeinflusst, indem Strahlung direkt über die Haut aufgenommen wird. Beim Menschen ist dies bedeutsam, weil aus der Aufnahme hochenergetischer UV-Strahlung Vitamin D in der Haut gebildet wird.
Dem Tageszyklus sind andere äußere Zyklen überlagert. Vor allem der Jahreszyklus ist wesentlich, der aus einem kompletten Umlauf des Planeten Erde um das Zentralgestirn Sonne resultiert. Dabei weist die Erdachse eine Neigung gegenüber der Bahnebene (Ekliptik) auf, in der sie um die Sonne rotiert. Dieser Schiefe der Ekliptik verdankt das terrestrische Leben die Jahreszeiten. Denn aus der Neigung resultiert eine unterschiedliche Beleuchtung der Hemisphären der Erde: die Sonnenstrahlen treffen zu unterschiedlichen Zeiten unter verschiedenen Winkeln auf der Erde auf (Ausnahme Äquator). Die Strahlung wird dann unterschiedlich von der Erdoberfläche absorbiert und reflektiert. Die wesentlichen Folgen sind Frühling, Sommer, Herbst und Winter. Während auf der Südhalbkugel Sommer ist, ist auf der Nordhalbkugel Winter. Die jahreszeitliche Schwankung der Erdeinstrahlung ist dabei nur der unmittelbare Aspekt. Aus ihr lassen sich beispielsweise Schwankungen der mittleren Temperatur und der Feuchtigkeit in betreffenden Erdregionen ableiten. Diese sekundären Faktoren beeinflussen ihrerseits die irdische Natur.
Der Mensch unterliegt jahreszeitlichen Stimmungsschwankungen. Die unterschiedliche Beleuchtung und Tageslänge zu verschiedenen Jahreszeiten führt zu "Frühlingsgefühlen" und "Winterdepressionen". Der Hormonhaushalt und die Psyche des Menschen werden von der Sonneneinstrahlung beeinflusst.
Tages- und Jahreszyklus sind nur ein kleiner Ausschnitt von periodischen Zeiträumen, die nachhaltig das irdische Leben beeinflussen. Auf der großen Zeitskala sind sicherlich die Quasiperioden von Eiszeiten und Zwischeneiszeiten zu nennen, die meines Wissens keiner exakten Periode genügen. Das Ineinandergreifen vieler Faktoren führt zu komplexen Wechselwirkungen im Klimahaushalt der Erde, die letztendlich nicht einfache Perioden wiedergeben.
Im Rahmen des biologischen Zeitbegriffs lässt sich festhalten, dass die Zeit unser Leben, unseren ganzen Tagesablauf, den Verlauf eines Jahres durch den Einfluss der Jahreszeiten (Strahlung, Temperatur, Feuchtigkeit) diktiert. Unser Biorhythmus unterliegt täglichen und jahreszeitlichen Schwankungen: Die Zeit beherrscht uns!

Die größte Skala in Längen und Zeiträumen gibt uns das Universum vor. Betrachtet man die Entwicklung des Universums im Rahmen der relativistischen Kosmologie, so ist das vielfach verifizierte Modell, das breite Zustimmung unter Astrophysikern erhält, das des Urknalls. Der Kronzeuge dieses Modells ist die kosmische Hintergrundstrahlung, die man in alle Richtungen an der Himmelssphäre gleichermaßen misst. Man interpretiert diese isotrope Strahlung als erste elektromagnetische Emission, die vom heißen, expandierenden Feuerball, unserem jungen Universum, abgestrahlt wurde. Die Hintergrundstrahlung ist ein Relikt aus einer Zeit, als es noch keine Galaxien gab, nicht einmal Sterne. Sie wurde frei, als sich die ersten Atomkerne mit Elektronen zu neutralen Atomen verbanden und damit das frühe Universum schlagartig durchsichtig für Strahlung wurde. Diese Epoche heißt Rekombinationsära und wird bei einer Zeit etwa 400000 Jahre dem Urknall datiert. Die Bewegung von Galaxien bezeugt ebenfalls den Urknall. Sämtliche extragalaktischen Systeme entfernen sich vom irdischen Beobachter. Diese Fluchtbewegung kennt man als Hubble-Effekt.
Im Urknall-Modell soll aus einem anfänglichen, sehr symmetrischen Zustand unendlich hoher Dichte und Temperatur, der Urknall-Singularität, unser beobachtetes Universum entstanden sein. Dieser Zustand hatte eine große Ordnung, so dass die Unordnung in der weiteren Entwicklung dieses Zustands nur zunehmen konnte. Physiker parametrisieren die Unordnung gerne durch eine thermodynamische Größe, die man Entropie nennt. Sie nimmt also bei der Entwicklung des Universums in komplexe, ungeordnete Strukturen zu. Auch das Urknall-Modell hat seine Probleme und wurde durch andere Zusätze (Inflation) oder neue Ansätze (Branen-Kosmologie, Ekpyrosis, Zyklisches Universum) modifiziert.
Ein wesentlicher Umstand ist nun in der Diskussion von Zeitbegriffen relevant. Das Urknall-Modell zeigt, dass offensichtlich unser Universum mit der Zeit expandierte und es weiterhin einer Expansion unterliegt. Diese Expansion kann mit dem Hubble-Parameter berechnet werden. Weit entfernte Quasare, eine Form sehr aktiver und heller Galaxienkerne, gestatten die Messung der Expansion auch zu frühen Entwicklungsphasen des Universums. Neben den Quasaren sind Galaxien hinzu getreten, die durch massereiche Galaxienhaufen im Vordergrund gelinst werden. Gravitationslinsen verstärken so leuchtschwache Galaxien, die an sich - ohne Linse - unbeobachtbar wären. Genau dies geschah beim aktuellen Entfernungsrekord einer Galaxie bei z = 10.
Aus diesen Beobachtungen leitet man ein kosmologisches Modell ab, dass ein dynamisches, expandierendes Universum hervorbringt. Demzufolge kann der Expansionsradius des Universums im jeweiligen Entwicklungszustand als Zeitparameter dienen. Den Expansionsradius, den man auch als Skalenparameter bezeichnet, könnte man als kosmologische Zeit bezeichnen. Der Expansionsradius ist jedoch nicht direkt astronomisch beobachtbar. Er folgt erst indirekt aus der Messung anderer kosmologischer Parameter (Dunkle Energie, Dunkle Materie, Hubble-Parameter) aus einem theoretischen, kosmologischen Modell.

Eine letzte Disziplin möchte ich augenzwinkernd anführen, die Politik. Hinter dem politischen Zeitbegriff verbirgt sich natürlich der bestimmende Zeitzyklus des politischen Lebens: die Legislaturperiode von vier Jahren. Man kann darüber streiten, ob dieser Zeitraum zu lange oder kurz ist. In jedem Falle ist es sehr instruktiv, teilweise amüsant bis grotesk, wenn sich die Legislaturperiode dem Ende eines Zyklus zuneigt und Wahlen neuer Repräsentanten anstehen. Besondere Erwähnung finden die Begriffe des Wahlversprechens und der Wahllüge. Sie werden von politischen Gegnern instrumentalisiert, um sich die neue Legislaturperiode zu sichern. Wer auch immer die Wahl "gewinnt", das ausgeklügelte System aus Regierung und Opposition sichert dem Volk mit multiplen Interessen in der Regel, eine gebührende Berücksichtigung aller Interessen. Dem Diktat des politischen Zeitbegriffs unterliegen glücklicherweise nur wenige Menschen, die Politiker selbst.

Zeitsysteme, Zeitskalen und Zeitmessung

Periodisch auftretende Ereignisse, wie der Lauf der Erde um die Sonne (Jahr), die Phasen des Mondes (Monat) oder die Rotation der Erde um die Sonne (Tag) bezeugen den direkten Einfluss der Umgebung und in diesem Sinne natürlicher Zyklen auf den vom Menschen benutzte Zeitmaße. Sämtliche Kalender beruhen auf diesen natürlichen Zeiteinheiten.
Neben den natürlichen Zyklen als Basis eines Zeitsystems wurden bald künstliche Zyklen eingeführt, die religiös, ideologisch, pragmatisch oder technisch motiviert waren. Die Erkenntnisse der Physik spielten bei der Zeitmessung eine wichtige Rolle und ermöglichten den Bau immer genauerer Uhren, die auch im industriellen Bereich relevant wurden. Präzise Zeitmesssysteme sind vitale Voraussetzung einer hochtechnisierten Zivilisation.

Einen wesentlichen Einfluss auf die Zeitsysteme hatten die Babylonier, eine der ersten Zivilisationsformen der Menschheitsgeschichte überhaupt. Dieses Volk war in Mesopotamien, dem Zweistromland zwischen den Flüssen Euphrat und Tigris und dem heutigen Irak angesiedelt. Ihre Kultur fußt auf den Babylonischen Zahlen, die nicht auf dem Dezimalsystem (Basis ist die Zahl 10), sondern auf dem Duodezimalsystem (Basis ist die Zahl 12) und dem Sexagesimalsystem (Basis ist die Zahl 60) beruhen. In der babylonischen Kultur galten die 12 und deren Vielfache, wie die 24 und die 60, als heilige Zahlen, die sich sowohl im babylonischen Alltagsleben als industrielles Zählmaß, als auch in der Architektur und Verzierung religiösen Stätten wieder finden.
Folgen wir nun der weiteren Einteilung in noch kleinere Zeiteinheiten, wie der Woche, der Stunde und der Minute. Die sieben Tage der Woche könnten darauf zurückgeführt werden, dass die hellsten Himmelsobjekte der Babylonier Sonne, Mond, Merkur, Venus, Mars, Jupiter und Saturn waren. Diese sieben Gestirne sind bequem mit dem bloßen Auge beobachtbar und verändern ihre Helligkeit, je nach räumlicher Nähe sowie relativer Stellung zu Erde und Sonne (Opposition, Konjunktion). Auch die ferneren Planeten Mars, Jupiter und Saturn können so signifikant an Helligkeit zunehmen und sogar die hellsten Sterne überstrahlen. Jedem dieser sieben sichtbaren Himmelsobjekte wurde ein Wochentag zugeordnet. Dieser Bezug hat in den indogermanischen Sprachen überdauert. Hier ist eine Auswahl von Untergruppen der indogermanischen Sprachfamilie - der Germanischen, Griechischen und Romanischen Sprachgruppe - die den Bezug von Wochentag und Himmelskörper belegen:

Samstag, engl. Saturday: Saturn (grch. Saturnos, röm. Saturnus)
Sonntag, engl. Sunday: Sonne (grch. helios, lat. sol)
Montag, engl. Monday, frz. lundi: Mond (lat. luna)
Dienstag, engl. Tuesday, frz. mardi: Mars (grch. Ares, röm. Mars)
Mittwoch, engl. Wednesday, frz. Mercredi: Merkur (grch. Hermes, röm. Merkur)
Donnerstag, engl. Thursday, frz. jeudi: Jupiter (grch. Zeus, röm. Jupiter)
Freitag, engl. Friday, frz. vendredi: Venus (grch. Aphrodite, röm. Venus)

Eine alternative Erklärung für die sieben Tage der Woche ist, dass zwischen aufeinander folgenden gleichen Mondphasen jeweils sieben Tage liegen. Weil es vier Mondphasen gibt hat der Monat daher (etwa) vier Wochen.
Die Unterteilung des Tages in 24 Stunden hängt auch mit den Babyloniern zusammen. Die 24 ist gerade das Doppelte der Zahl 12 und ebenfalls eine heilige, babylonische Zahl. So ist der 24 Stunden-Tag bereits seit dem 7. Jahrhundert v.Chr. nachweisbar.
Die feinere Einteilung der Minute in 60 Sekunden folgte wesentlich später. Schriften belegen, dass dies erst in der spätrömischen Epoche etabliert wurde. Dadurch erklärt sich, dass wir bis heute die Stunde in 60 Minuten, die Minute in 60 Sekunden, das Grad in 60 Bogenminuten und die Bogenminute in 60 Bogensekunden einteilen.
In Praxi hatten die Zeitmaße Minute und Sekunde keine Relevanz. Die Zeitmessung wurde erst nach dem Mittelalter, in der Neuzeit, so genau, dass Minute und Sekunde Einzug ins tägliche Leben fanden. Der Beginn der Neuzeit wird mit der (vermeintlichen) Entdeckung Amerikas 1492 durch den italienischen Seefahrer Cristoforo Colombo (1446 - 1506), besser bekannt unter Christoph Kolumbus, datiert. Bereits um 1000 n.Chr. hatten die Wikinger Amerika entdeckt.

Die Zeitmessung war anfangs recht primitiv: die ersten Uhren basierten auf der Messung des scheinbaren Laufs der Sonne, strömenden Flüssigkeiten oder Sand. Die Sonnenuhr nutzt den scheinbaren Lauf der Sonne am Himmelsgewölbe (aufgrund der Erdrotation) aus, um - Tageslicht und nahezu wolkenloser Himmel vorausgesetzt - die Tageszeit zu bestimmen. Der Schattenwurf eines aufgerichteten Stabes, dessen Neigung an die geographische Breite angepasst sein sollte, dient dann als Zeitmesser.
altgrch. Klepshydra: Wasseruhr Seit dem 3. Jahrtausend v.Chr. benutzte man auch Wasseruhren, Öluhren und Sanduhren. Allen gemein ist das Prinzip, dass ein gleichmäßig strömendes Medium in einer bestimmten Zeit eine fixierte Strecke passiert. Man musste jedoch zuvor diese Uhren an einem anderen Zeitmesser eichen. Die Klepshydra (grch. kleptein: stehlen und hydro: Wasser) war eine bekannte Wasseruhr in der griechischen Antike. In ihr wurden die hydrostatischen und hydrodynamischen Kenntnisse verwertet, die insbesondere Archimedes (285 - 212 v.Chr.) und sein Schüler Ktesibios fanden. Das Prinzip ist dem der Sanduhr ähnlich, nur dass ein Schwimmer die Höhe einer in ein Gefäß eingeströmten Flüssigkeit markiert. Diese Höhe ist ein Maß für die bereits verstrichene Zeit.
Eine modernere Uhr wurde erst im 17. Jahrhundert entwickelt: die Pendeluhr. Das Zeitmessprinzip erfuhr eine wichtige Änderung, denn nun wurden nicht mehr gleichmäßig strömende Medien herangezogen, die in endlicher Zeit eine Fallstrecke zurücklegten, sondern periodische Prozesse. Das hatte den Vorteil das die Uhr beliebig lange Zeiten messen konnte, wenn man dafür sorgte, dass der Taktgeber eine langfristig stabile Schwingung mit nahezu konstanter Periodendauer hatte.
Gleichsam wurde mit der Pendeluhr ein fundamentales Uhrenprinzip begründet, nämlich dass moderne Uhren immer aus einem Taktgeber und einem Zählwerk bestehen. Während der Taktgeber, wie das Pendel, die Schwingung immer wieder aufs Neue durchläuft, zählt das Zählwerk die durchlaufenen Schwingungen und gibt sie an eine Anzeigevorrichtung, wie dem Zeiger, weiter. Rein mechanische Uhren wurde dann mit einer schwingenden Feder, der Unruh, versehen, die eine neue Form von Taktgeber wurde. Bei darauf folgenden elektronischen Uhren, wie der Quarzuhr, ist der Taktgeber ein schwingender Quarzkristall. Quarz zeigt den piezo-elektrischen Effekt, das heißt beim Anlegen einer elektrischen Spannung wird der Kristall deformiert. Legt man nun eine Wechselspannung an, so geschieht diese Deformation periodisch in entgegengesetzte Richtungen: Der Quarzkristall oszilliert permanent mit der Periode der Wechselspannung und kann als Taktgeber genutzt werden.
Die modernste und bisher präziseste Form einer Uhr ist die Atomuhr. Die Idee zur Atomuhr äußerte erstmals der amerikanische Physiker und Chemiker Willard Frank Libby (1908 - 1980) im Jahre 1946. 1948 wurde die erste Atomuhr hergestellt, die mit Ammoniak (NH₃) funktionierte. Das Element Cäsium (Cs) erwies sich als geeigneter und so wurde 1955 die erste Cäsium-Atomuhr gebaut. Das verwendete Isotop Cäsium-133 hat den Vorteil, dass es nicht radioaktiv ist. Der Taktgeber bei Atomuhren ist elektromagnetische Strahlung. Gemäß der klassischen Elektrodynamik handelt es sich dabei um ein im Raum sich ausbreitendes elektromagnetisches Feld, bei dem elektrisches und magnetisches Feld sich abwechselnd gegenseitig induzieren. Deshalb brauchen elektromagnetische Wellen kein Trägermedium wie beispielsweise Schall, der Luft oder Wasser benötigt. Elektromagnetische Strahlung kann sich im Vakuum fortpflanzen. Aber was schwingt bei den Cäsiumatomen überhaupt? Cäsium kann nur einen von zwei möglichen energetischen Zuständen annehmen, der mit dem Gesamtspin des Cäsiumatoms zusammenhängt. Der Spin ist eine Eigenschaft, der aus einer speziell relativistischen Behandlung der Quantenmechanik resultiert (Theorie des Quantenphysikers Paul Dirac). Anschaulich wird der Spin mit einem Eigendrehimpuls interpretiert, was nur eine veranschaulichende Hilfsvorstellung ist. Zwischen diesen beiden Spinzuständen, man nennt sie Hyperfeinstrukturniveaus, kann das Cäsiumatom elektromagnetische Übergänge machen. Der Übergang kann durch Emission oder durch Absorption von elektromagnetischer Strahlung (Photonen) bewerkstelligt werden, je nach Spinstellung. Man bringt nun die Cäsiumatome in Form eines Atomstrahls in das Innere eines Hohlraumresonators. Zuvor hat magnetische Selektion (wie im Stern-Gerlach-Versuch) stattgefunden, so dass man den Spinzustand des eingebrachten Cäsiums kennt. Im Hohlraumresonator herrscht ein hochfrequentes Wechselfeld in Form von Mikrowellen. Diese "klappen die Spins um", bewerkstelligen also einen Hyperfeinstrukturübergang bei Cäsium-133 und bringen sie damit in einen anderen energetischen Zustand. Bei einer bestimmten Schwingungsdauer des Mikrowellenfeldes werden besonders viele Spins umgeklappt. Dies ist der Resonanzfall. Die Schwingungsdauer des elektromagnetischen Feldes ist dann sehr kurz, die damit assoziierte Frequenz also recht hoch. Die Frequenz beträgt 9.19 GHz und entspricht gerade einer Wellenlänge von 32.6 mm. Genau genommen sind es 9 192 631 770 Schwingungen pro Sekunde, die das Mikrowellenfeld ausführt, um die Atome des Isotops Cäsium-133 anzuregen. Genau dies wird als Taktgeber in Atomuhren genutzt! Die Zeitmessung ist damit so genau, dass man die Sekunde über dieses Cäsiumnormal 1967 definiert hat. Über Funk steuert die Cäsium-Atomuhr der Physikalisch-Technischen Bundesanstalt (PTB) in Braunschweig Funkuhren an, die sich so selbsttätig nachkorrigieren und umstellen.

In der Astrophysik gibt es ebenfalls sehr genaue Taktgeber: die Pulsare. Es handelt sich dabei um schnell rotierende Neutronensterne, die aus dem Gravitationskollaps eines massereichen Sterns hervorgegangen sind. Aufgrund des Drehimpulserhaltungssatzes verliert der kollabierende Stern kaum an Rotation, so dass durch die Verkleinerung des Trägheitsmomentes noch schnellere Rotationszeiten für den Neutronenstern resultieren. Das ist vergleichbar mit dem Eiskunstläufer, der sich schneller dreht, wenn er die Arme eng am Körper anlegt ("Pirouetteneffekt"). Die Millisekundenpulsare haben Rotationszeiten im Bereich von Millisekunden (Crab-Pulsar im Sternbild Stier z.B. nur 33 ms). Weil ihre Periode ebenfalls sehr stabil bleibt, könnten sie auch als Taktgeber herhalten. Problematisch wird es sicherlich dann, wenn man eine solche Uhr am Arm tragen möchte...

Ein interessanter letzter Aspekt bei der Zeitmessung ist die radiogene Altersbestimmung. Diese Methode entwickelte ebenfalls Willard Frank Libby, der dafür auch den Nobelpreis für Chemie 1960 erhielt. Man nutzt bei diesem Verfahren den Zerfall einer radioaktiven Substanz (Radionuklid), wobei nach Ablauf einer Halbwertszeit nur noch die Hälfte der Ausgangsmenge des Radionuklids vorhanden ist. Besonders bekannt ist die Radiokarbon-Methode oder C-14-Methode, die besonders bei Bestimmung des Alters von organischem Material benutzt wird. Man verwendet das Isotop C-14 des Kohlenstoffs (C), das in organischen Substanzen häufig vorkommt ("Biologie ist Kohlenstoffchemie"). Radioaktives C-14 und nicht radioaktives C-12 kommen normalerweise in einem festen Mischungsverhältnis in der Natur vor. Dieses Mischungsverhältnis übernehmen Lebewesen, die beispielsweise Kohlenstoff in Form von Kohlendioxid mit der Atmung oder mit der Nahrung im Körper aufnehmen. Stirbt jedoch das Lebewesen, bleibt anfangs das Mischungsverhältnis zwar erhalten, mit dem Altern des Kadavers wird es jedoch gestört: der Anteil von Kohlenstoff-14 wird immer geringer, weil er radioaktiv zerfällt. Findet man nun totes, organisches Material, muss man nur aus organischen Proben das Verhältnis von C-12 zu C-14 bestimmen. Ein Vergleich dieses Probenverhältnisses mit dem konstanten Verhältnis in der Natur lässt dann über das Zerfallsgesetz und die bekannte Halbwertszeit auf das Alter der organischen Substanz schließen. Die Halbwertszeit von 5730 Jahren bei C-14 legt fest, dass diese Methode für einen zurückliegenden Zeitraum von 500 bis 50 000 Jahren tauglich ist.
Das gleiche Prinzip nur mit einem anderen Radionuklid wird in der Datierung von Gesteinen verwendet. Bei den Blei-Methoden findet man eine Anreicherung von Blei im Gestein, das ein radioaktives Zerfallsprodukt von Uran (U-235, U-238) oder Thorium (Th-232) sein kann. Die Halbwertszeiten liegen auf einer - vergleicht man es mit C-14 - ungleich größeren Skala von Milliarden von Jahren. Die Halbwertszeit bei der Rubidium-Strontium-Methode beträgt sogar 50 Milliarden Jahre. Mit dieser Methode wurde der bisher älteste, irdische Gesteinsfund datiert (Kanada, 2002): 3.825 Milliarden Jahre! Bei Mondgesteinen funktionieren die genannten Methoden auch, so dass man ein Mindestalter von 4.5 Milliarden Jahre für den Mond ableiten konnte. Alle Methoden der radiogenen Altersbestimmung sind von unschätzbarem Wert für die Archäometrie.

Dieser Abschnitt hat gezeigt wie vielfältig die Zeit Einzug in das kulturelle und technologische Leben des Menschen gehalten hat. Zeitskalen und Zeitmesssysteme gibt es in mannigfacher Ausprägung. Manche Zeiteinheiten sind schon so alt, dass es für den modernen Menschen in Vergessenheit geraten ist, woher sie stammen. Und doch sind sie ein ganz natürlicher Bestandteil unseres Alltags geworden, so zum Beispiel die Zeitmaße Stunde und Minute.
Im nächsten Abschnitt soll es nun um den Zeitbegriff selbst gehen. Zeit scheint, auch wenn man sie messen kann, etwas Merkwürdiges zu sein, das wir im alltäglichen Leben völlig anders wahrnehmen, als sie tatsächlich ist.

Historische Entwicklung des Zeitbegriffs

Ein sicheres Fundament für den Zeitbegriff bietet die Naturwissenschaft. Die wesentliche Disziplin ist die Physik, die ich aufgrund ihrer zentralen Rolle für den Zeitbegriff bei den disziplinären Zeitbegriffen ausgelassen habe. Bis zum modernen, relativen Zeitbegriff war es jedoch ein langer Weg. Bis heute ist diese moderne, naturwissenschaftliche Auffassung von Zeit keine alltägliche Selbstverständlichkeit. Im Gegenteil: Viele Laien leben heute noch mit dem antiken, absoluten Zeitbegriff. Dies liegt natürlich daran, dass die Relativität der Zeit im Alltag nie in Erscheinung tritt. Auch aus diesem Grund hat die Revolutionierung des Zeitbegriffs bis ins 20. Jahrhundert gedauert. Im Alltag lässt es sich recht gut mit einer absoluten Zeit leben.

Schwierig gestaltet sich eine wissenschaftliche Definition des Zeitbegriffs und die Kenntnis ihrer Natur. Die ersten Versuche begannen - wie so oft - bei den alten Griechen in der Antike. Sie urteilten vom Standpunkt der alltäglich erfahrbaren Welt aus und glaubten, dass die Zeit einen absoluten und einen nicht beeinflussbaren Charakter hat. Diese Vorstellung geht auf Aristoteles (384 - 322 v.Chr.), einem Schüler Platons (der wiederum Schüler von Sokrates war), zurück. Er ging davon aus, dass der natürliche Zustand eines Körpers die Ruhe sei und er sich erst bewege, wenn eine Kraft auf ihn wirke. Diese Auffassung von Zeit überdauerte zwei Jahrtausende. Denn zu diesem Schluss kam auch Isaac Newton (1643 - 1727) im 17. Jahrhundert, als er die klassische Mechanik begründete und 1687 die "Principia mathematica" veröffentlichte. Das Newtonsche Gesetz besagt, dass sich ein Körper beschleunigt bewegt und zwar proportional zu der wirkenden Kraft auf den Körper. Der absolute Ruhezustand oder eine absolute Position blieb jedoch schleierhaft. In der Newtonschen Theorie gibt es keinen ausgezeichneten Punkt: verschiedene Beobachter konnten behaupten, dass sie sich in Ruhe relativ zu einem bewegten System befänden und beide hätten recht. Eine andere Problematik war, dass die Kräfte in der Newtonschen Theorie instantan, also ohne Verzögerung, wirkten. Auch für die Ausbreitung von Licht wurde lange vermutet, dass sie instantan verläuft. Der dänische Astronom Ole R�mer (1644 - 1710) konnte jedoch bereits 1676 anhand von Beobachtungen der Verfinsterungen des Jupitermondes Io zeigen, dass die Lichtgeschwindigkeit endlich ist und etwa 224 000 km/s betragen solle. Dies liegt zwar unter dem heute gemessenen Wert von knapp 300 000 km/s, war aber eine enorme Leistung von R�mer, da es einerseits wider die damals vorherrschende wissenschaftliche Lehrmeinung war und andererseits das Messprinzip an sich recht simpel, doch genial war. Eine Theorie für die Ausbreitung von Licht begründete James Clerk Maxwell 1865 mit der klassischen Elektrodynamik. In dieser Theorie vereinigte er Elektrizität und Magnetismus, die bis dato nicht miteinander in Zusammenhang gebracht wurden. Aus den Differentialgleichungen der Elektrodynamik kann man mit wenig Aufwand eine Wellengleichung extrahieren. Es handelt sich gerade um die Gleichung, die die Fortpflanzung elektromagnetischer Wellen beschreibt. Die Geschwindigkeit dieser Wellen, die Lichtgeschwindigkeit c, sollte konstant sein. Die Phasengeschwindigkeit der elektromagnetischen Wellen hängt vom optischen Medium ab und ist im Vakuum am größten. Ungeklärt war aber, auf welcher Trägersubstanz sich diese elektromagnetischen Wellen ausbreiten sollten. Man kannte bereits die Schallwellen der Akustik, die sich in einem Trägermedium wie Luft oder Wasser ausbreiten. Ohne Medium keine Schallwelle. Was war nun die Trägersubstanz von Licht?
Das Michelson-Morley-Experiment sollte darüber 1881 und in verbesserter experimenteller Anordnung 1887 Klarheit verschaffen. Hier versuchte man die Trägersubstanz, den "Äther" des Lichts, nachzuweisen. Dazu verwendete man ein Michelson-Interferometer (Abbildung), das einen Lichtstrahl an einem halbdurchlässigen Spiegel aufspaltet. Der Aufbau ist so konzipiert, dass der so aufgespaltene Strahl Lichtwegen folgt, die senkrecht zueinander sind. Nach einer gewissen Laufstrecke werden die Teilstrahlen an Spiegeln total zurück reflektiert, wieder zusammengeführt und mithilfe von Interferenz (Überlagerung der Wellen) analysiert. Die Idee ist nun, dass bei Existenz des Äthers als Lichtträgermedium, dieser auf den unterschiedlichen Lichtwegen unterschiedlich stark durch die Erdrotation abgelenkt werden sollte. Die Lichtgeschwindigkeit sollte deshalb auf den beiden Wegen unterschiedlich sein. Michelson und Morley konnten jedoch nur gleiche Lichtgeschwindigkeiten messen. Das Experiment scheiterte also insofern, dass man den Lichtäther nicht nachweisen konnte. Oft wird behauptet, Albert Einstein sei durch dieses Experiment inspiriert worden. Er war jedoch bei Ausgang des zweiten Experiments (1887) erst acht Jahre alt. Er wurde auch daraufhin gefragt, ob ihn das Resultat des Michelson-Morley Experiments beeinflusst habe, was er verneinte.
Ein anderer Sachverhalt war viel gewichtiger: Bereits mit 16 Jahren (1895) fand Einstein eine Inkonsistenz zwischen Maxwells Elektrodynamik und der Newtonschen Gravitationstheorie. Gemäß Newton sollten alle Prozesse gleich ablaufen, egal ob ein System ruhe oder sich gleichförmig bewege. Der Fachbegriff für dieses Verhalten lautet Galilei-Invarianz. Maxwells Gleichungen hingegen zeichneten ein Bezugssystem aus, nämlich das, in dem der Äther ruht. Sobald sich das System relativ zum Äther bewegt, veränderten die Maxwell-Gleichungen ihre Form: sie waren nicht Galilei-invariant!
Diese Inkonsistenz inspirierte Einstein zu seiner weltberühmten Arbeit "Von der Elektrodynamik bewegter Körper" (1905), der Grundlage der Relativitätstheorie. Er zeigte darin auf, dass der "Licht-Äther" überflüssig sei, wenn man bereit sei, die Vorstellung einer absoluten Zeit (und eines absoluten Raums) fallen zu lassen! Mit diesem drastischen Schritt konnte er die Inkonsistenzen in der Newtonschen Theorie bereinigen, was aber schwerwiegende Folgen für das physikalische Weltbild hatte. Die Sichtweise veränderte sich insofern grundlegend, dass Zeit einen nichtlinearen und nicht globalen - also lokalen - Charakter hat! Ähnliches gilt für den Begriff der Länge, die eine Abhängigkeit vom Bewegungszustand erfuhr (Lorentz-Kontraktion). Die Relativität von Länge und Zeit sind eine zwingende Konsequenz der in allen Bezugssystemen konstanten Lichtgeschwindigkeit. Die Lichtgeschwindigkeit ist absolut! Den resultierenden, völlig neuartigen Zeitbegriff kann man in der disziplinären Klassifikation als physikalische Zeit einordnen.

"Absolutheit der Lichtgeschwindigkeit bedingt Relativität von Länge und Zeit."

Blicke in die Vergangenheit

Die Endlichkeit der Lichtgeschwindigkeit schafft bereits die Voraussetzung für eine Reihe von Konsequenzen, der wir uns im Alltag in der Regel nicht bewusst sind. Wenn sich die Informationen, die ständig über das Auge in unser Bewusstsein dringen, mit begrenzter Geschwindigkeit ausbreiten, so sehen wir ständig Dinge, die schon vergangen sind. In der Regel ist der zeitliche Abstand dieser Ereignisse nicht sonderlich hoch. Denn das Licht breitet sich außerordentlich schnell aus. Knipst man einen Lichtschalter an, so wird der Raum mit kaum messbarer Verzögerung erhellt. Für unser Empfinden wird er sogar instantan hell. Licht breitet sich im Vakuum mit einer Geschwindigkeit von fast 300 000 Kilometern pro Sekunde oder gut einer Milliarde Stundenkilometern aus. In einer Sekunde legt das Licht also in etwa die Distanz von der Erdoberfläche zum Mond zurück. Anders gesagt, der Mond ist eine Lichtsekunde entfernt.
Dies motiviert zu einer anderen Sichtweise: Wie sehr die Geschehnisse in der Vergangenheit liegen, hängt davon ab, wie weit sie vom Betrachter entfernt sind. Der morgendliche Blick in den Spiegel in ein verschlafenes Antlitz zeigt uns, wie wir vor zwei Nanosekunden (Milliardstel Sekunden) aussahen. Der 100m-Läufer am Start sieht die Ziellinie, wie sie vor einer Drittel Mikrosekunde aussah. Von einem drei Kilometer entfernten Berg sieht man das zehn Mikrosekunden alte Bild. Das Abbild des Mondes liegt wie gesagt eine gute Sekunde in der Vergangenheit, wenn wir den Mond betrachten. Das Licht der Sonne benötigt von ihrer Oberfläche etwa acht Minuten, bis es an der Erde ankommt. Kosmische Distanzen lassen tiefe Blicke in die Vergangenheit zu. So hat der nächste Stern, Proxima Centauri, eine Entfernung von 4.3 Lichtjahren. Strahlung, die wir von ihm empfangen ist 4.3 Jahre alt. Das Zentrum der Milchstraße, von uns aus im Sternbild des Schützen (Sagittarius) gelegen, hat eine Entfernung von etwa 25 000 Lichtjahren. Das Licht, das wir heute aus dem Galaktischen Zentrum beobachten und analysieren, wurde zu einem Zeitpunkt ausgesandt, als auf der Erde Steinzeitmenschen, wie der Cro-Magnon Mensch, lebten. Das Entfernteste, das wir mit bloßem Auge wahrnehmen können, ist die Andromedagalaxie, eine Begleitgalaxie der Milchstraße. Ihr heute empfangenes Licht zeigt sie, wie sie vor 2.2 Millionen Jahren aussah! Die aktuell am weitesten entfernte Galaxie beobachten Astronomen bei einer kosmologischen Rotverschiebung von zehn. Bei Zugrundelegung eines kosmologischen Modells bekannter Dunkler Energie und Dunkler Materie bedeutet dies, dass die Galaxie bereits 480 Millionen Jahre nach dem Urknall existierte! Aufgrund der kosmologischen Rotverschiebung beobachtet man diese Quelle im Bereich infraroter Strahlung, obwohl die Strahlung "vor Ort" ultraviolett ist. Die Galaxie befindet sich in einer Phase heftiger Sternbildung.
Das Entfernteste, was Menschen überhaupt detektieren können, ist die kosmische Hintergrundstrahlung. Sie kann allerdings keinem scharf abgebildeten Objekt zugeordnet werden. Es ist eine diffuse Mikrowellenstrahlung, die - wie bereits unter den disziplinären Zeitbegriffen beschrieben - aus der Frühphase des Universums stammt. Diese Rekombinationsstrahlung wurde ausgesandt, als das Universum gerade 550 000 Jahre alt war. Für den irdischen Beobachter war das vor mehr als 13 Milliarden Jahren!

Es ist deshalb klar, das Teleskope "Zeitmaschinen" sind: Je weiter bzw. tiefer man in das Universum blickt, umso älter sind die beobachteten Objekte. Die Astronomie hat deshalb immer einen paläoastronomischen Aspekt. Das ist ein großer Vorteil, denn so können Astronomen kosmische Objekte in verschiedenen Entwicklungsstadien beobachten und sie durch geeignete Entwicklungsszenarien miteinander verknüpfen. Letztlich führt dies auf Vorstellungen davon, wie sich das Universum als Ganzes entwickelt haben könnte. Dies ist Gegenstand der Kosmologie.

Relativität der Zeit

Endliche Lichtgeschwindigkeit und ihre Konstanz in jedem Bezugssystem ist eines der Grundpostulate der Relativitätstheorie. Der Verlauf der Zeit hängt deshalb vom Bezugssystem und Bewegungszustand (Spezielle Relativitätstheorie, SRT, 1905) und von der Position in Bezug auf Quellen von Gravitation ab (Allgemeine Relativitätstheorie, ART, 1915). Zahlreiche Experimente haben die Richtigkeit dieser Aussagen bestätigt: Für relativistisch bewegte Teilchen, d.h. Teilchen, die sich mit Geschwindigkeiten bewegen, die der Lichtgeschwindigkeit vergleichbar sind, ist der Ablauf der Zeit verlangsamt. Anders gesagt sind Zeitintervalle im Beobachtersystem gedehnt. Dieses Phänomen bezeichnet man als Zeitdilatation (lat. dilatare: ausdehnen).
Eine spezielle Form von Elementarteilchen, die Myonen, die verwandt sind mit den Elektronen (nur etwas schwerer) sind Bestandteil der kosmischen Strahlung. Diese Strahlung kommt von verschiedenen kosmischen Quellen und trifft auf die Atmosphäre der Erde. Dort löst sie Kaskaden von Teilchenreaktionen aus, aber manche Teilchen durchlaufen die Atmosphäre auch ungehindert. Die Myonen bewegen sich dabei mit relativistischen Geschwindigkeiten und können daher trotz ihrer kurzen Lebensdauer, die ihnen eine Nachweisbarkeit auf der Erdoberfläche verbieten sollte, nachgewiesen werden. Denn die Zeitdilatation der SRT dehnt Zeitintervalle im mitbewegten Myonensystem, die Eigenzeit, um den Lorentz-Faktor. Dieser Faktor ist essenziell in der Speziellen Relativitätstheorie und wird bei relativistischen Geschwindigkeiten deutlich größer als 1. In der Zeitdilatation der SRT darf er als Zeitdehnungsfaktor aufgefasst werden. Ein festes Zeitintervall im Myonensystem misst ein externer Beobachter also vergrößert.
Die masselosen Photonen übertrumpfen die massebehafteten Myonen noch. Sie bewegen sich exakt mit der Lichtgeschwindigkeit, so dass der Lorentz-Faktor gegen unendlich geht: Photonen altern nicht, sie existieren in einer zeitlosen Welt. Das lässt das Wesen von Licht noch rätselhafter erscheinen, als es ohnehin - auch in der Physik - ist.

Erschwerend hinzu kommt, dass die Zeit mit dem Raum auf komplizierte Weise eine Einheit bildet, das Raum-Zeit Kontinuum oder die Raumzeit. Die Lorentz-Transformation ist die adäquate Operation, um physikalische Größen in gegeneinander bewegten Bezugssystemen zu vergleichen. Mathematisch zeigt sich hier eine Vermischung von Raum- und Zeitkoordinaten, eine gegenseitige Abhängigkeit. Zeit ist also entgegen dem alltäglichen Empfinden eng verwandt mit dem Raum und nicht unabhängig von ihm zu sehen. In der vierdimensionalen Raumzeit sind die drei Raumkoordinaten und die Zeitkoordinate vollkommen gleichberechtigt und untrennbar miteinander verknüpft. Aus diesem Grund kann man die wahre Natur der Zeit nur diskutieren, wenn man den Raum berücksichtigt.
Dies geschieht im Rahmen der Allgemeinen Relativitätstheorie. Die Konzepte dieser Theorie haben weitreichende Folgen für den Zeitbegriff in Gravitationsfeldern - wie schon am Beispiel der Erde klar wird. Messungen mit hochpräzisen Atomuhren belegen, dass die Zeit im Tal langsamer verrinnt als auf Bergen. Dies ist auch bekannt als Gravitationsrotverschiebung oder (gravitative) Zeitdilatation der ART. Die Sanduhr ist eine wunderbare Metapher für eine wesentliche Aussage der ART: Gravitation, die den Sand im Stundenglas nach unten rinnen lässt, bestimmt selbst den Ablauf der Zeit! In der Allgemeinen Relativitätstheorie gibt es außer dem Lorentz-Faktor weitere Korrekturfaktoren für die Zeitdilatation, die von der Form der gekrümmten Raumzeit, der Metrik, abhängen. Diese Faktoren variieren, je nachdem, ob die Erde, die Sonne, ein Neutronenstern oder ein Schwarzes Loch den Zeitfluss verändern.

Der Zeitablauf oder das Zeitmaß ist also für verschiedene Beobachter im Allgemeinen sehr unterschiedlich. Bewegungszustand und Nähe zu Massen, die Raumzeitkrümmungen hervorrufen, beeinflussen das Zeitmaß. Daher wird klar, dass mit der Relativitätstheorie auch der Begriff der Gleichzeitigkeit seinen Sinn verlor. Die Zeit an verschiedenen Punkten der Welt läuft unterschiedlich schnell ab. Der Begriff der Zeit macht nur lokal einen Sinn oder in einem recht flachen Gebiet der Raumzeit, wie der Erde. Da dies im Allgemeinen nicht gegeben ist, muss man von einem relativen Charakter des Zeitbegriffs sprechen.

Schlangen im Weltraum

Ein kurzes Wort zum Untertitel: Nein, es handelt sich nicht um eine Fortsetzung der Reihe "Schweine im Weltall", wie sie in der Muppet-Show bekannt wurde. Es handelt sich vielmehr um eine neue Sicht von Raum und Zeit, verknüpft in der Raumzeit, die man sich auch sehr plastisch vor Augen führen kann.
Typischerweise nehmen wir uns und alle Gegenstände als dreidimensionale Gebilde wahr, die eine Länge, eine Breite und eine Höhe haben. Diese 3D-Objekte bewegen sich in der Zeit. Das war schon Newtons Sichtweise. Die zeitliche Entwicklung oder Dynamik spiegelt sich in Bewegungsgleichungen wider. Diese beschränkte Perspektive scheint vom Gehirn diktiert zu sein. Unsere Wahrnehmung hat sich so entwickelt, dass wir die Raumzeit aufspalten in Raumdimensionen und Zeitdimension. 3D-Objekte bewegen sich in der Zeit.
Auf der Grundlage der Kenntnis dieser vier Dimensionen könnte man die Struktur der Raumzeit ganz anders darstellen - bereits ohne Relativitätstheorie. Man könnte nämlich die Raumkoordinaten (oder eine davon) über der Zeitkoordinate skizzieren. In Weg-Zeit-Diagrammen in der Schulphysik ist dies eine der leichtesten Übungen. Man betrachte beispielsweise eine Kugel, die eine schiefe Ebene hinabrollt. Die Aufgabe besteht nun darin, immer nach Ablauf von einer Sekunde den auf der Ebene zurückgelegten Weg zu messen. Jedes Paar aus so gewonnener Zeitkoordinate und Wegabschnitt trage man in einem Weg-Zeit-Diagramm auf. Es ergibt sich eine Linie. Die Steigung (1. Ableitung nach der Zeit) der Linie im jeweiligen Punkt entspricht übrigens der Momentangeschwindigkeit der Kugel. Die Krümmung (2. Ableitung nach der Zeit) ist die Beschleunigung. Wesentlich ist nun die Struktur der Linie. In ihrem Steigungsverhalten und ihrer Krümmung steckt bereits sehr viel an Information über die Dynamik dieses einfachen Systems. Die Linie hat Schlangenform und windet sich im Diagramm.
Wir könnten nun den typischen Tagesablauf eines Menschen in analoger Weise visualisieren. Er steht morgens auf, bereitet sich vor für den Arbeitstag, gelangt zur Arbeitstelle, arbeitet, macht sich auf den Nachhauseweg und geht vielleicht noch einkaufen und kehrt am Abend zurück. Dargestellt als Punkt, der sich auf der Oberfläche des Erdglobus bewegt, ist diese Bewegung relativ kompliziert. Der Punkt möge überall auftauchen, wo unser arbeitender Protagonist war. Es ergäbe sich eine recht komplexe Struktur der Raumzeit. Unter Berücksichtigung aller Dimensionen wird der 3D-Mensch zur 4D-Schlange ("Serpensifikation"). Wir schlängeln uns also durch die Raumzeit.

Diese einfachen, alternativen Visualisierungsmethoden entschleiern die Raumzeit als komplexe Skulptur. Sie ist durchzogen von Weltlinien, den Schlangen, die sich bewegende Weltpunkte oder Ereignisse hinterlassen. Mit jedem neuen Zeitabschnitt erlangt diese Skulptur eine neue Form, eine zusätzliche Komplexität.
Im Rahmen der Newtonschen Physik stellt sich die Gestalt der Skulptur für jeden Beobachter als die gleiche dar (identische Koordinatensysteme vorausgesetzt). In der Relativitätstheorie wird dies modifiziert: die äußere Form ist abhängig vom Bezugssystem. In beiden Theorien bleibt die Skulptur jedoch glatt und kontinuierlich. Das ändert sich, wenn die Zeit Sprünge macht, dazu aber erst später.

Zeitreisen und Zeitpfeile

Zeit ist mathematisch gesehen ein Skalar, hat demnach nur einen Betrag. Eine simple Zahl gibt uns Auskunft darüber wie viel Uhr es ist oder wie viel Zeit seit Christi Geburt verstrichen ist. Die tägliche Erfahrung lehrt auch, dass man sich zwar in den Raumdimensionen ohne weiteres vor und zurück bewegen kann, dies aber in der Zeitdimension nicht gelingt. Eine Reise mit einer Zeitmaschine in großem Umfang ist bisher nicht gelungen, obwohl dazu eine Reihe von Überlegungen angestellt wurden. Ich darf anmerken, dass Zeitreisen in sehr geringem Umfang jedoch eine alltägliche Sache sind! Das wird klar, wenn man sich nochmals die Konzepte der Relativitätstheorie vor Augen führt. Im Rahmen der Speziellen Relativitätstheorie folgt, dass der Zeitablauf in bewegten Systemen verlangsamt, dilatiert, wird. Steige ich also ins Auto und fahre eine Weile kann ich mit Recht behaupten, weniger gealtert zu sein, als ein Beobachter, der vor Ort verblieben ist. Anders gesagt: Ich bin um winzige Sekundenbruchteile in die Zukunft gereist.
Unter Berücksichtigung der Allgemeinen Relativitätstheorie kann man behaupten, dass Bewohner im Tal weniger altern, als Bergbewohner. Denn je näher man einer großen Masse, der Erdmasse ist, umso langsamer verstreicht die Zeit. Reist man vom Tal in die Berge, geht die Reise also in die Zukunft. Reist man hingegen von den Bergen ins Tal, geht es in die Vergangenheit.
Wir reden hier nur von Sekundenbruchteilen. Es ist aber schon erstaunlich, welche Auswirkungen eine nicht globale, nicht absolute Zeit hat. In großem Maßstab sind Zeitreisen deshalb schwierig, weil die erforderlichen Relativgeschwindigkeiten (SRT) bzw. kompakten Massen (ART) enorm sind. Erst bei Relativgeschwindigkeiten, die fast der Lichtgeschwindigkeit entsprechen oder kompakten Massen, die vergleichbar mit Schwarzen Löchern sind, sind die Effekte und gereiste Zeitintervalle groß.
Beschränkt man sich darauf, nur ein paar Blicke in die Vergangenheit zu werfen, ohne selbst auf die Vergangenheit Einfluss nehmen zu können, so ist dies möglich, wie an verschiedenen Beispielen ausgeführt wurde.

Das, was wir jeden Tag beobachten, dass ein Tag beständig dem vorangegangenen folgt, nennt man den Zeitpfeil. Zeit hat eine Richtung (ist aber trotzdem mathematisch kein Vektor!). Man unterscheidet verschiedene Zeitpfeile in der Physik, je nachdem, aus welchem theoretischen Sachverhalt sie sich ableiten. Nachfolgend möchte ich diese vorstellen.

Die Kausalität ist ein Indikator für die Zeitrichtung: die Ursache kommt vor der Wirkung. Das definiert den kausalen Zeitpfeil. Wenn wir einen Film sehen, der ohne unser Wissen rückwärts abgespielt wird, wird nach kurzer Zeit klar, dass die Geschehnisse in der umgekehrten Reihenfolge ablaufen. Die Kausalität ist alltägliche Erfahrung. Als weiteres Beispiel möge eine Tasse dienen, die vom Tisch fällt, und auf dem Boden in Scherben zerspringt. Der umgekehrte Fall wurde noch nie beobachtet, dass Scherben vom Boden auf den Tisch springen und spontan eine Tasse formen (wenngleich das sehr praktisch wäre). Das ist aus thermodynamischen Gründen verboten oder anders ausgedrückt in Wahrscheinlichkeiten extrem selten, praktisch unmöglich. Diese Irreversibilität lässt sich mit dem fundamentalen 2. Hauptsatz der Thermodynamik begründen. Die Entropie ist ein Maß für die Unordnung in einem System. Sie kann bei Zustandsänderungen in einem abgeschlossenen System nicht abnehmen. Bei einem Übergang von einem geordneten Zustand in einen ungeordneten, nimmt die Entropie zu. Der Betrag der Entropie verrät daher die Zeitrichtung, es sei denn sie bleibt konstant. Dies nennt man den thermodynamischen Zeitpfeil oder entropischen Zeitpfeil. Er steht in enger Beziehung zum kausalen Zeitpfeil.

Der elektromagnetische Zeitpfeil hängt mit der Ausbreitung von Lichtwellen zusammen. Eine bewegte Ladung strahlt elektromagnetische Wellen ab. Diese Lichtwellen breiten sich nur in die Zukunft aus (retardierte Welle) und nicht in die Vergangenheit, obwohl es die Maxwell-Gleichungen zulassen würden. Die Gleichungen der Elektrodynamik sind zeitumkehrinvariant, d.h. sie unterscheiden nicht zwischen Vergangenheit und Zukunft. Ebenso ist es bei (bisher nicht nachgewiesenen) Gravitationswellen, also Krümmungen der Raumzeit, die sich mit der Lichtgeschwindigkeit ausbreiten. Auch sie propagieren nur in die Zukunft.
Elektromagnetische Wellen und Gravitationswellen sind daher Indikatoren für die Zeitrichtung.

Zeitpfeile zwängen unsere Lebensplanung in ein Korsett und charakterisieren in besondere Weise die Zeit. Zeitpfeile grenzen die Zeitdimension auch von den Raumdimensionen ab. Während man sich im Raum vor und zurück bewegen kann, gelingt das in der Zeit nicht - zumindest im Rahmen konservativer Physik. Zusammen mit der psychologischen Zeit und der thermodynamischen Zeit bildet die kosmologische Zeit die drei grundsätzlichen Zeitpfeile.

Erzeugung und Vernichtung

Mit der Quantentheorie wurde ein sehr erfolgreicher, mathematischer Apparat eingeführt, der es gestattet Teilchen an einem bestimmten Ort zu einer bestimmten Zeit zu erzeugen oder zu vernichten. Die mathematischen Gebilde, die das leisten heißen Erzeugungsoperatoren und Vernichtungsoperatoren. Im Rahmen der Zweiten Quantisierung beschreibt man jedes quantentheoretische Problem in diesem Formalismus. Dabei genügen Erzeugungs- und Vernichtungsoperatoren bestimmten mathematischen Relationen, den kanonischen Kommutatorrelationen. Ein Teilchen wird in der Quantentheorie repräsentiert durch eine Wellenfunktion, einer räumlichen und im Allgemeinen zeitlichen Verteilung. Die Wellenfunktion kann auch komplexwertig sein. Das Absolutquadrat der Wellenfunktion ist gerade ein Maß für die Aufenthaltswahrscheinlichkeit des beschriebenen Teilchens in Raum und Zeit. Prominentes Beispiel sind die Elektronenschalen im Atom. Die Elektronen werden durch Wellenfunktionen beschrieben. Das führt letztendlich dazu, dass es keine klassischen Punktteilchen sind (Bohr-Atommodell), die um den Atomkern kreisen, sondern verschmierte Elektronenwolken, die Orbitale. Angeregte Zustände des Elektrons im Atom kann man erzeugen, indem man den Erzeugungsoperator auf den energetisch niedrigeren Zustand, z.B. den Grundzustand, des Elektrons anwendet.
Mit diesem Werkzeug der Erzeugungs- und Vernichtungsoperatoren ist eine erkenntnistheoretische Neuinterpretation der klassischen Teilchenbahn verbunden. Klassisch bewegt sich ein Teilchen auf einer kontinuierlichen Bahn. Vom Anfang bis zum Ende der Bahn ändert sich das Teilchen nicht. Es ist immer dasselbe Teilchen in dieser klassischen Bewegung. In der Zweiten Quantisierung kann man sich aber vorstellen, dass die Bewegung des Teilchens dadurch entsteht, dass es an dem einen Ort vernichtet wird, während es zu einem fortgeschrittenen Zeitpunkt an einem nächsten Punkt der Bahn erzeugt wird. Die Bahn ist also kein kontinuierlicher Fluss, sondern sie ist in kleine Stücke zerhackt: die Bahn ist diskret! Pointiert kann man sagen: Das Teilchen ist nicht mehr dasselbe, allenfalls das gleiche.
Was hat dieser quantentheoretische Exkurs mit dem Zeitbegriff zu tun? Nun, wie, genauer in welcher Reihenfolge, die Erzeugungs- und Vernichtungsoperatoren entlang der Bahn auf eine Ausgangswellenfunktion angewendet werden müssen, kann durch den Zeitentwicklungsoperator parametrisiert werden. Er versieht die Erzeugungs- und Vernichtungsoperatoren gewissermaßen mit einer Zeitmarke. Die Zeit als Ordnungsparameter ist also eine wichtige Größe, auch in der Quantentheorie.

Zeitlose Physik

Mit der Quantentheorie verbinden sich noch weitere Aspekte zum Thema Zeit. Bekanntlich beeinflusst schon der quantenmechanische Messprozess Quantensysteme! Eine Beobachtung ist damit bereits invasiv und verfälscht ein "objektives Ergebnis". In der Quantentheorie ist der lokale Beobachter unumgänglich. Auf ihn werden die Observablen bezogen und ausgewertet. Zeit hat also auch im praktikablen Sinne der Quantentheorie einen relativen, nämlich einen lokalen Charakter.
Ein anderer Gesichtspunkt ist ein schon lange bekannter Quanteneffekt: die Heisenbergsche Unschärferelation. Man kennt sie in ihrer Formulierung als Orts-Impuls-Unschärfe, was bedeutet, dass je genauer ich den Ort eines Teilchens kenne, umso ungenauer wird die Aussage über den Impuls des Teilchens. Die Unschärferelation kann aber auch als Energie-Zeit-Unschärfe formuliert werden. Dann bestimmt sie die zeitlichen Fenster für Energiefluktuationen im Quantenvakuum. Anders gesagt ist festgelegt, für welchen Zeitraum man den Energieerhaltungssatz verletzen darf, um sich einen bestimmten Energiebetrag aus dem Quantenvakuum zu "leihen". Große Energiebeträge können nur sehr kurz bereitgestellt werden, während es für kleine Energiebeträge für längere Zeiträume möglich ist. Wendet man dieses Prinzip auf die Darstellung einer Teilchenbahn im Phasenraum (Darstellung Impuls über Ort) an, so zeigt sich, dass die klassisch determinierte Phasenraumbahn zur quantenmechanisch undeterminierten Teilchenwelle verschmiert wird. Die Zeit ist also eine Größe, die mit einer gewissen Unsicherheit behaftet ist. Dieses Maß an Unsicherheit hängt von der kanonisch konjugierten Größe zu der Zeit ab, der Energie.

Man kann noch weiter ausholen, dringt aber dabei in kompliziertere Bereiche der Quantentheorie vor. Die fundamentale Schrödinger-Gleichung der Quantentheorie beschreibt eindeutig die Dynamik der Wellenfunktion, also deren zeitliche Entwicklung. Lösungen der Schrödinger-Gleichung verraten also den Zustand des Quantensystems zu einem beliebigen Zeitpunkt. Eine relativistische Formulierung dieser Schrödinger-Gleichung kennt man als die Wheeler-DeWitt-Gleichung. Sie ist auch Gegenstand der Quantenkosmologie.
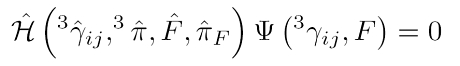Man erhält diese Gleichung, wenn man die Einsteinsche Relativitätstheorie in Hamiltonsche Form umschreibt. Dieser Zugang ist bereits in der klassischen Mechanik bekannt, besitzt jedoch eine so allgemeine Formulierung, dass man ihn auch auf andere Theorien übertragen kann. Die Wheeler-DeWitt-Gleichung ähnelt formal der stationären Schrödinger-Gleichung zu einem Energieeigenwert null. Die Lösungen sind Wellenfunktionen des quantenmechanischen Systems, das den Kosmos als Ganzes beschreibt. Pointiert spricht man häufig von der "Wellenfunktion des Universums". Sie ist auf einem unendlich-dimensionalen Superraum der Raumzeit-Geometrien und aller Materiefelder definiert.
In der Quantenkosmologie gibt es auch den vertrauten Apparat der kanonischen Quantisierung der üblichen Quantentheorie. So kann man Vielteilchenzustände, Baby-Universen genannt, aus Vakuumzuständen, Voids genannt, durch Anwendung von Erzeugungsoperatoren erzeugen. Allerdings wird die zugehörige Wheeler-DeWitt-Gleichung noch komplexer und sogar nicht-linear, weil Wechselwirkungen zwischen diesen Zuständen berücksichtigt werden müssen. Die quantenmechanische Teilchenerzeugung und -vernichtung entspricht in dieser Anwendung auf den Kosmos der Erzeugung und Vernichtung von Universen! Der erkenntnistheoretische Inhalt dieser Theorie ist immens, denn unser Universum wäre kein ausgezeichnetes, sondern eine Realisierung unter vielen. Die Quantenkosmologie prognostiziert Muliversen. Diese Szenarien laufen auch unter dem Stichwort Viele-Welten-Theorie.

Kommen wir nach dieser recht theoretischen Betrachtung zurück zum Zeitbegriff. Erstaunlicherweise ist Wheeler-DeWitt-Gleichung in ihrer fundamentalen Formulierung unabhängig vom Parameter Zeit! Die Zeitabhängigkeit tritt in der Wheeler-DeWitt-Gleichung weder explizit noch implizit auf. Es gibt zwar einen Zeitparameter, der die Blätterung (Foliation) der Raumzeit in Unterräume niedrigerer Dimension (Hyperflächen) bestimmt. Die Foliation ist jedoch vollkommen willkürlich! Daher ist auch der resultierende Zeitbegriff nicht eindeutig. Es muss nun untersucht werden, ob die Quantentheorien verschiedener Foliationen in dieselbe Physik münden. Die Wahl einer Foliation kann man als "Eichung" im Sinne der Eichtheorien auffassen. Sind verschiedene Foliationen unitär äquivalent, so führen sie auf gleiche physikalische Gleichungen. Dann wäre die gewählte Foliation irrelevant.
Zur Gewinnung spezieller Lösungen der Wheeler-DeWitt-Gleichung muss man den lokalen Beobachter wieder einführen. Deshalb resultiert wieder ein Ordnungsparameter, den man mit einem Zeitbegriff identifizieren kann. Dies führte in der Vergangenheit zu der Frage nach einer "Physik ohne Zeit". Die Frage ist nun, inwiefern diese Hypothese haltbar ist, wenn man bei einer praktikablen Umsetzung von "zeitlosen Theorien" wieder auf den Zeitbegriff stößt.

Verlassen wir das Gebiet der Quantenkosmologie und wenden uns nur der Relativitätstheorie zu. Die Zeitlosigkeit ist - aufgrund von Effekten der Speziellen Relativitätstheorie, wie beschrieben - auch ein Charakteristikum von Teilchen, die sich lichtschnell bewegen. Solche Teilchen tragen den Oberbegriff Luxonen. Dazu gehören das Photon, das elektromagnetische Wechselwirkungen überträgt, also das Lichtteilchen selbst; das hypothetische Graviton, das bei gravitativen Wechselwirkungen ausgetauscht werden soll und das Gluon, das die starke Wechselwirkung vermittelt und daher wichtig für die Kernphysik ist. Diese Teilchen "erleben" wegen ihrer hohen Geschwindigkeit keine Zeit. So manch gestresster Manager, der sich einen Tag mit mehr als 24 Stunden wünschte, wird neidvoll auf die Luxonen schauen: Bei ihnen hat der Tag mehr Stunden, noch besser, es gibt gar keinen Tag mehr!

Sprünge der Zeit

Die Zeit wird üblicherweise als kontinuierlich wahrgenommen. Der metaphorische Begriff des Zeitflusses geht auf Aristoteles zurück. Er begründete eine Sichtweise des stetigen Zeitbegriffs, der auch die Relativitätstheorie und selbst die Quantentheorie überdauerte. Es gab zwar zahlreiche Versuche, die Zeit in der Quantentheorie zu diskretisieren, also zu quantisieren, doch sie scheiterten alle.
Eine neue Theorie revolutioniert diese Sichtweise. Es handelt sich um die Loop-Quantengravitation (dt. auch Schleifenquantengravitation). Dieses theoretische Konstrukt folgt, wenn man die Konzepte der Allgemeinen Relativitätstheorie mit denjenigen der Quantenmechanik vereint. Die Konsequenzen dieses Zugangs sind drastisch: sie resultieren in einer Granulation der Raumzeit und in einer Quantisierung der Zeit in Zeitquanten.
Eine Schwierigkeit besteht darin, dass die Allgemeine Relativitätstheorie in einem völlig neuen mathematischen Formalismus formuliert wird. Die Basis dieses Apparats sind die Ashtekar-Variablen, die erst 1986 begründet wurden. Die quantentheoretischen Methoden sind ganz ähnlich wie im üblichen Hamilton-Formalismus. Ein Eigenwertproblem führt auf das Spektrum des Hamilton-Operators. Dabei entdeckte man fundamentale Einheiten des Raums, die Volumenquanten und Flächenquanten. Anders gesagt ist die Raumzeit gekörnt! Die typischen Größenordnungen befinden sich auf der Planck-Skala und sind außerordentlich klein: die Körnung ist extrem fein, denn jedes Korn durchmisst nur 10^-33 Zentimeter. Entsprechend hat ein Volumenquant ein Volumen von 10^-99 Kubikzentimetern.
Um ein Gefühl für die Planck-Skala zu bekommen, kann man das Elektron heranziehen. Nach den modernen Konzepten der Quantenfeldtheorien gehört das Elektron zur Teilchengruppe der Leptonen und ist punktförmig. Klassisch kann man jedoch dem Elektron eine Ausdehnung zuschreiben, den klassischen Elektronenradius. Er beträgt nur 2.8 x 10^-13 Zentimeter. Das entspricht aber gewaltigen 10²⁰ Planck-Längen!
Ebenso ist die Zeit in fundamentale Einheiten eingeteilt. Die Zeitquanten haben eine Länge, die vergleichbar ist mit der Planck-Zeit, also etwa 10^-43 Sekunden. Diese Quantisierung der Zeit kann man sich gut am Beispiel des Tickens einer Uhr vergegenwärtigen. Zeit ist gemäß der Loop-Quantengravitation kein kontinuierlicher Zeitfluss, sondern sie besteht aus Zeitsprüngen. Ein 100m-Läufer bewegt sich schnappschussartig vom Start ins Ziel. Ein Elementarteilchen im Teilchenbeschleuniger springt auf der Beschleunigungsstrecke auf Planck-Längen in Planck-Zeiten. Bewegungen ähneln eher der Fortbewegung eines Froschs.
Die Raumzeit als Schlangen-Skulptur verliert in der Loop-Quantengravitation ihre Kontinuität. Die Skulptur ist nicht glatt, sondern rau und auf der Planck-Skala granular. Wie im Pointilismus, einer Maltechnik im Impressionismus, setzt sich das Gesamtbild aus vielen kleinen Punkten zusammen, die räumlich einen Durchmesser von 10^-33 Zentimetern haben.
Die Loop-Quantengravitation ist eine relativ neue physikalische Theorie. Im Gegensatz zur Relativitätstheorie und zur Quantentheorie hat sie sich noch nicht bewährt. Deshalb ist bisher nicht gesichert, ob die Zeit in oben beschrieben Weise diskretisiert ist. Wie bei allen Theorien gilt es nun, diesen eleganten Vorschlag eines Konzepts durch geeignete Hypothesen am Experiment zu testen. Erst nach einer Reihe erfolgreich bestandener Tests wird sich die revolutionäre Sichtweise der Schleifenquantengravitation behaupten können.

Implikationen aus der Physik

Das bisher Gesagte ist nur eine Ansammlung von Beobachtungen, von Ideen, von neuen Erkenntnissen über die Zeit. Doch was ist ihre wahre Natur? Können wir diese wahre Natur im Sinne einer platonischen Idee überhaupt begreifen? Oder ist Zeit nur eine Illusion, die unsere Gehirne uns vorgaukeln?

Die moderne Physik deutet an, dass man auf einen Zeitbegriff verzichten könnte. Quantenkosmologie und Loop-Quantengravitation sind keine Standardtheorien, erst recht keine Theorien, die sich bewährt haben. Aber es sind interessante "Spieltheorien", die Spekulationen des Möglichen freilegen. Tests müssen zeigen, ob diese Theorien auch etwas mit der Natur zu tun haben, die uns umgibt. Zunächst muss man als Theoretiker glücklich sein, dass man einen Ansatz gefunden hat, der weiter verfolgt werden kann. Faszinierend ist der Gedanke, dass auf einer höheren Verständnisebene der Zeitbegriff verschwinden mag, während er auf niedriger, alltäglicher Ebene unser Dasein kontrolliert.

Beschränkt man sich auf den Horizont bewährter Theorien, so stellt man fest, dass die Relativitätstheorie neue Denkansätze über die Natur der Zeit offenbart. Dies gilt sowohl im alltäglichen Kontext, als auch - erst recht - auf der kosmischen Ebene. Ein relativistisches Universum mit nur lokal ablaufender Zeit legt eher den Gedanken nahe, dass unsere "irdische Zeit" eine Insel unter vielen im Ozean der Ewigkeit ist. Lyrisch formuliert es Jean Paul so:

"Die Zeit ist eine Larve der Ewigkeit."

Strenggenommen ist der Ablauf der Zeit überall anders! Wir verdanken es nur der relativ flachen Raumzeit auf der Erde und der Tatsache, dass wir uns mit Geschwindigkeiten weit unterhalb der Lichtgeschwindigkeit bewegen, dass wir weltweit einen ähnlichen Ablauf der Zeit haben und der Begriff Gleichzeitigkeit Sinn macht.
Albert Einstein sagte "Die Zeit ist das, was man auf einer Uhr ablesen kann.". Diese lakonische Stellungnahme ist natürlich im relativistischen Sinne richtig: jeder Beobachter kann eine Uhr mit sich führen und behaupten, dass sei der Ablauf der Zeit. Es gibt keinen übergeordneten Beobachter, der eine absolute Zeit messen könnte: Zeit ist eine relative Größe. Jedes Individuum hat sein eigenes, ganz persönliches Zeitmaß. Insofern besitzt Zeit messbare Realität.
Dass Zeit nur eine (vom Menschen gemachte) Illusion ist, scheint eine unhaltbare Aussage zu sein. Jeder neue Tag, jedes Ticken einer Uhr und jedes fallende Sandkorn im Stundenglas zeugen vom Verrinnen der Zeit. Unsere Erinnerung bezeugt Vergangenes, die Geschichtsbücher dokumentieren historische Ereignisse. Wir erwarten zukünftige Ereignisse, die auch eintreten. Wo ist da Platz für eine Illusion?

Philosophische Aspekte

Springen wir fast 2500 Jahre zurück, in die antike Philosophie Platons. Auch von dieser Richtung lässt sich die Frage nach der Natur der Zeit angehen: Existiert Zeit als platonische Idee, losgelöst von allem Materiellem? Vielleicht ist es das Schicksal des Menschen, wie das der Gefangenen im Höhlengleichnis nie die wahre Natur der Zeit schauen zu können.
Diese Aspekte der platonischen Erkenntnistheorie führt Immanuel Kant (1724 - 1804) zwei Jahrtausende nach Platon fort. Er spricht von dem Ding an sich (Noumenon), das durch Wahrnehmungsprozess (Sinne) und Erkenntnisprozess (Verstand) zur Erscheinung (Phaenomenon) verformt wird. Diese Begriffe stehen im gleichen Gegensatz zueinander wie Schein und Wirklichkeit.
Die Philosophie kreist seit Jahrtausenden im Rahmen der Erkenntnistheorie um dieses Begriffspaar. Die Frage lässt sich auch als Subjekt-Objekt-Problem formulieren: Worin besteht das Verhältnis von erkennendem Menschen (Subjekt) zum erkannten Ding (Objekt)? Wenden wir diesen Subjekt-Objekt-Formalismus auf das Thema dieses Essays an, so stellen wir die Frage nach dem Verhältnis von demjenigen, der Zeit verstehen möchte zu der Zeit selbst. Eine Auflösung bestünde im Verständnis der Zeit.

In der Philosophie kennt man unterschiedliche Strömungen, unter anderem Positivismus, Rationalismus, Sensualismus und Empirismus. Ihr Verhältnis zu Zeitbegriffen kann man wie folgt erörtern.
Der Positivist sieht in den Grenzen der Erfahrung auch die Grenzen der Erkenntnis. Damit bezieht er eine Gegenposition zum Rationalisten. Die Beschränkung seines Erfahrungsbereiches auf die Erde würde eine generelle Diskussion des Zeitbegriffs, beispielsweise auf der Stufe quantenkosmologischer Konzepte, schnell beenden. Ähnlich ist es bei den Sensualisten: sie sehen die Wirklichkeit in Empfindungsinhalten, z.B. in einem Gefühl. Der psychologische Zeitbegriff ist also derjenige, der sensualistisch gefolgert werden würde. In radikaler Form gipfelt der sensualistische Empirismus in George Berkeleys Ausspruch esse est percipi ("Sein ist Wahrgenommenwerden"). Damit negiert der Sensualist jede transzendente Existenz und würde sich allen Zeitbegriffen, die über den psychologischen Zeitbegriff hinausgehen, verweigern. Der Positivist wendet sich ebenfalls von einer Diskussion transzendenter, nicht erfahrbarer Sachverhalte ab.
Der Physiker ist eher der rationalistischen Position zugewandt: er nutzt und entwickelt physikalische Theorien, die es ihm nicht nur gestatten Zeit im alltäglich erfahrbaren Bereich, sondern auch in Grenzbereichen (relativistische Geschwindigkeiten, starke Gravitationsquellen, subatomare Skala) zu beschreiben, die alltäglich nicht oder sogar niemals erfahrbar sind. Die Betonung liegt hier auf dem Begriff beschreiben, denn verstehen liegt bereits eine Erkenntnisstufe höher. Das "Warum ist Zeit so?" ist bereits eine Frage, die im interdisziplinären Bereich zwischen Physik und Philosophie anzusiedeln ist.

Das Verständnis von Zeit ist damit eine Frage der Grundhaltung. Sicherlich kann der größte Teil der Menschheit sehr gut damit leben, dass die Zeit im Alltag als absolute Zeit erscheint, weil typische Geschwindigkeiten weit unterhalb der Lichtgeschwindigkeit liegen bzw. die Raumzeit auf der Erde nahezu flach ist. Die relative Zeit tritt bei einigen wenigen anspruchsvollen Techniken zutage, wie der Satellitenkontrolle und dem GPS. Der Reiz besteht aber im erkenntnistheoretischen Zugewinn, was Zeit eigentlich ist bzw. ob es sie überhaupt gibt, oder sie eine Illusion ist, die sich der Mensch in seinem erinnerungsfähigen Denken macht.
Gibt es nun die Zeit? Gibt es sie nur, weil es einen Beobachter gibt, der sich an Vergangenes erinnern kann? Ist die Frage nach der Natur der Zeit eine erneute Manifestation des anthropischen Prinzips, das verkürzt besagt: "Wir sehen das Universum wie es ist, weil wir hier sind, um es zu sehen."? Dies wäre zumindest eine interessante These. Wenn dem so wäre, so verhält es sich ähnlich wie es Elias Canetti in einem Aphorismus formulierte:

"Ein niederschmetternder Gedanke: dass es vielleicht überhaupt nichts zu wissen gibt; dass alles Falsche nur entsteht, weil man es wissen will."

Dieses Bonmot kann man auch auf den manipulativen Charakter des quantenmechanischen Beobachters beziehen: die Messung, also das Erwerben von Wissen, verändert den zu messenden Sachverhalt. Sicherlich gilt dieses Prinzip auch in einer Quantenkosmologie, denn nach dem kosmologischen Prinzip gelten die irdisch verifizierten Quantengesetze auch für den Kosmos als Ganzes und dessen Wellenfunktion.

Resümee

Wir müssen uns wohl zunächst mit dem Gedanken anfreunden, dass Antworten auf die Frage nach der Natur der Zeit auch mit modernen physikalischen Konzepten uns einen Rest von Unklarheit lassen. Zeit ist in jedem Fall eine relative Größe - eine Aussage, die sich sowohl im psychologischen als auch physikalischen (relativistischen) Zeitbegriff widerspiegelt. Die Relativität kann in extremer Form zum Verschwinden des Zeitablaufs und somit des Zeitbegriffs führen, wie die Diskussion der Quantenkosmologie, der Loop-Quantengravitation und die lichtschneller Teilchen nahe legt. Typische Fragestellungen der Physik, seien sie auf dem Gebiet der Quantentheorie oder der Relativitätstheorie, kommen aber um einen Zeitparameter nicht umhin.

Der physikalische Zeitbegriff muss weiter erforscht werden. Eine tiefe Hoffnung liegt in neuen übergeordneten Theorien, wie einer Quantengravitation, einer gelungenen Synthese aus Relativitätstheorie und Quantentheorie. Vielleicht ist die Loop-Quantengravitation der richtige Ansatzpunkt, was zukünftige Experimente erweisen werden. Fraglich ist jedoch - und das deuten bereits Überlegungen zur Wheeler-DeWitt-Gleichung an - inwiefern die Konzepte potenzieller Zeitbegriffe verstehbar und auf die alltäglich erfahrbare Welt übertragbar sind. Die häufig anzutreffende Tendenz der Unanschaulichkeit oder Befremdlichkeit findet man bereits in vielen Bereichen der modernen Physik. Nichtsdestotrotz können Physiker wahre, verifizierbare Aussagen über die Natur ableiten. Eine Reihe moderner Technologien nutzt bereits exzessiv die Erkenntnisse der "unanschaulichen Physik" und stützt deren Richtigkeit.
Die moderne Physik stellt mathematische Apparate und Modelle zur Verfügung, die relativ unanschaulich sind und - angemessen interpretiert - unser Weltbild und unser Verständnis der dinglichen Welt auf eine harte Probe stellen.

"Wir bezahlen mit der Anschaulichkeit und gewinnen den Preis der Erkenntnis."

Vereinfacht gesagt besteht die Schwierigkeit im Verständnis des Zeitbegriffs in einem Skalenproblem: der Mensch befindet sich auf der intermediären mesoskopischen Skala, das ist seine alltäglich erfahrbare Welt. Auf der mikroskopischen Skala regieren die Gesetze der Quantentheorie. Hier gibt es mesoskopisch unverständliche Prozesse, wie den Tunneleffekt, Unschärfe, das Quantenvakuum oder manipulative Messungen. Auf der anderen Seite, der makroskopischen Skala, findet man die Gesetze der Relativitätstheorie. Auch hier findet man mesoskopisch seltsam anmutende Effekte, wie Zeitdilatation, Lorentz-Kontraktion, Raumzeitkrümmung und Gravitationslinsen. Zu allem Überfluss gibt es auch Überlappungsbereiche der großen Theorien (die Domäne der Quantengravitation): relativistisch schnelle Elementarteilchen, Teilchenbildung am Ereignishorizont Schwarzer Löcher (Hawking-Strahlung), Schwarze Löcher im Miniformat in Teilchenbeschleunigern oder - bestes Beispiel - die Quantenkosmologie.
Daraus wird schnell ersichtlich, weshalb die klassischen Theorien der Physik (Mechanik, Elektrodynamik, Thermodynamik) auf der mesoskopischen Skala liegen: sie waren schlicht einfacher zugänglich und anschaulicher, weil sie leicht in die Alltagswelt zu übertragen sind. Lange Zeit, bis zum Beginn des 20. Jahrhunderts, hat der mesoskopische Standpunkt und die "alltaggewöhnte Perspektive" den erkenntnistheoretischen und naturwissenschaftlichen Blick beschränkt und bedurfte eines Genies vom Kaliber Einsteins und Plancks, um diese Fesseln des Wissens zu sprengen. Doch selbst fast hundert Jahre nach dem Aufkommen der beiden großen Theorien, Relativitätstheorie und Quantentheorie, ringt der Mensch um ein Verständnis. Alte Begriffe wandeln sich, lösen sich auf, werden ersetzt oder neu definiert. Eine Hauptproblematik besteht sicherlich darin, dass menschliche Begrifflichkeiten mesoskopischem Denken entsprungen sind und nicht ohne weiteres oder gar nicht auf andere Skalen übertragen werden können. Deshalb darf es nicht verwundern, wenn sich herausstellen könnte, dass der Zeitbegriff nur dort Sinn macht, wo er erfunden wurde: Der bewohnten Erde, die sich im langsamen und flachen Sektor der Relativitätstheorie bewegt.

"Zeit vergisst man, wenn man Schönes erlebt."

Andreas Müller

Literatur

H. Goenner: Einführung in die Kosmologie (1994), Spektrum Akademischer Verlag
J.R. Gott: Zeitreisen in Einsteins Universum (2001), Rowohlt Taschenbuch Verlag
W. Misner, K.S. Thorne und J.A. Wheeler: Gravitation (1973), Freeman San Francisco
R. d'Inverno: Introducing Einstein's Relativity (1992), Oxford University Press
Schülerduden Philosophie (2002), Dudenverlag
Schülerduden Die Astronomie (1989), Meyers Lexikonverlag
T. Bührke: Albert Einstein (2004), Deutscher Taschenbuch Verlag
H.D. Zeh: Quantentheorie und Web Essays
Lee Smolin: Atoms of Space and Time, Scientific American, Januar 2004
A. Bauch: Wie funktioniert eine Atomuhr?, NaKlar!, wissenschaft-online
I. Schmidt-Mappes: Warum hat die Stunde 60 Minuten?, NaKlar!, wissenschaft-online
M.P. Streck: Mesopotamien

pdf pdf

nach oben

Start - Web-Artikel - Lexikon - Vorträge - Ausbildung - Essays - Rhetorik - Links - Autor - Kontakt

Impressum