Im Jahr 1609, also vor genau 400 Jahren, veröffentlicht der Johannes Kepler in Prag ein Buch unter dem Titel »Astronomia nova« (Neue Astronomie). Es enthält zwei Gesetze über die Bewegung der Planeten, die durch eine »magnetische Kraft« auf ihrer Bahn um die Sonne gehalten werden; zehn Jahre später ergänzt er sie noch durch ein weiteres Gesetz. Kepler selbst bezeichnet sie nie als »Gesetze«; für den tief religiösen Menschen ist die Welt von Gott nach einem mathematischen Plan geschaffen worden (ähnliches findet man bereits bei Plato und Pythagoras). Kepler geht es bei seinen Forschungen allein darum, Gottes Schöpfung zu verstehen, und die von ihm entdeckten »Gesetze« sind nach seiner Überzeugung nur ein Ausdruck der Weltharmonie (Harmonices mundi – Titel des Werks aus dem Jahr 1618): »Ich fühle mich von einer unaussprechlichen Verzückung ergriffen ob des göttlichen Schauspiels der himmlischen Harmonie. Denn wir sehen hier, wie Gott gleich einem menschlichen Baumeister, der Ordnung und Regel gemäß, an die Grundlegung der Welt herangetreten ist.«

• Die Planeten bewegen sich auf ellipsenförmigen Bahnen, in deren einem Brennpunkt die Sonne steht.
• Die Verbindungsstrecke zwischen Sonne und Planet überstreicht in gleichen Zeitabschnitten gleich große Flächen.
• Die Quadrate der Umlaufzeiten der Planeten sind proportional zu den dritten Potenzen der mittleren Entfernung zur Sonne.

Johannes Kepler stammt aus einfachen Verhältnissen: Der Vater, ein Söldner, verlässt die Familie, als das Kind fünf Jahre alt ist; die Mutter betreibt das Gasthaus des Großvaters. Der kränkliche Junge darf eine Lateinschule in Leonberg sowie Klosterschulen in Adelberg und Maulbronn besuchen; mit 18 Jahren studiert er Evangelische Theologie an der Universität Tübingen. Mathematik und Astronomie sind normale Bestandteile des Theologiestudiums; so kommt es, dass er durch seinen Mathematiklehrer Michael Maestlin vom neuen Weltbild des Domherrn Nikolaus Kopernikus erfährt und bald von dessen Richtigkeit überzeugt ist.

Wegen seiner nicht immer konformen Ansichten hat der junge Theologe keine Chance auf eine akademische Laufbahn an der durch orthodoxe Lutheraner beherrschten Universität. So wechselt er mit 23 Jahren als Lehrer für Mathematik und Moral an die evangelische Stiftsschule in Graz; nebenher erstellt er astrologische Prognosen. Berühmtheit erlangt er, als er in einem Horoskop einen kalten Winter und den Einfall türkischer Heere zufällig richtig vorhersagt.

Sein Ruhm als erfolgreicher Astrologe trägt dazu bei, dass er 1597 eine Schrift mit dem Titel »Mysterium Cosmographicum« (Das Weltgeheimnis) veröffentlichen kann; darin beschreibt er die Sonne im Zentrum eines Systems mit den bekannten sechs Planeten. Dass die Sonne (nach damaliger Erkenntnis) sechs Planeten hat und dass es genau fünf platonische Körper gibt, ist nach Keplers Überzeugung Teil eines göttlichen Plans. Die von Kopernikus ermittelten Verhältnisse der Bahnradien führen ihn zu einem mathematischen Modell, bei dem sechs Kugeln und die fünf platonischen Körper ineinander geschachtelt sind: Die Umlaufbahn des Saturn verläuft auf einer Kugel, der einen Würfel (Hexaeder) einschließt; in diesem ist wiederum eine Kugel enthalten, auf der die Umlaufbahn des Jupiter liegt; in diese Kugel passt genau ein Tetraeder, auf deren Inkugel sich der Mars bewegt; dann folgen Dodekaeder, Oktaeder und Ikosaeder, die jeweils Kugeln mit den Umlaufbahnen von Erde, Venus und Merkur einschließen. Abweichungen der Umlaufbahnen von der Kreisform erklärt Kepler (zu dieser Zeit noch) mit einer gewissen Dicke der Kugelschalen. Das Werk endet mit der Lobpreisung Gottes, der ihm die Gnade dieser Einsicht in seine Schöpfung gewährt hat. Sein Werk schickt er unter anderem auch an Galilei, mit dem er in den folgenden Jahren im Kontakt bleibt.

Im gleichen Jahr heiratet er Barbara Mühleck, Tochter eines Müllers; in den 14 glücklichen Ehejahren werden vier Kinder geboren, von denen nur zwei überleben. Im Rahmen einer Welle der Gegenreformation wird er 1600 aus dem katholischen Graz vertrieben, findet dann aber eine Stelle als Mathematik-Assistent des Astronomen Tycho Brahe in Prag; beide ergänzen sich auf glückliche Weise: Brahe ist ein glänzender Beobachter – der fehlsichtige Kepler ein brillanter Mathematiker.

Allerdings vertreten beide unterschiedliche Weltbilder: Brahe erkennt zwar auch, dass das Weltbild des Ptolemäus nicht mehr zu halten ist; er entwickelt jedoch ein eigenes Modell, das »zwischen« dem des Kopernikus und dem des Ptolemäus steht: Im Mittelpunkt des Systems steht die Erde; um sie kreisen Mond und Sonne; die (übrigen) Planeten drehen sich um die Sonne. Zwischen beiden entwickelt sich eine merkwürdige Rivalität: Einerseits hofft Brahe, dass seine Theorien durch Keplers mathematische Fähigkeiten bestätigt werden können, befürchtet aber andererseits, dass dieser seine Daten für eigene Forschungen benutzen könnte; daher gibt er ihm nur einen eingeschränkten Einblick in seine Unterlagen. Als Brahe dann unter ungeklärten Umständen stirbt, wird Kepler dessen Nachfolger als kaiserlicher Hof-Mathematiker (und Hof-Astrologe) und kann endlich alle Beobachtungsdaten nutzen. Bei der Umlaufbahn des Mars findet er Abweichungen von einer kreisförmigen Umlaufbahn von (nur) acht Bogenminuten, folgert daraus aber richtig, dass sich der Mars nicht auf einer Kreisbahn, sondern auf einer elliptischen Bahn um die Sonne bewegt (und auch die anderen Planeten). Er entwickelt die Kegelschnittlehre des Apollonios von Perge (260 – 190 vor Christus) weiter und beschreibt als Erster die Kegelschnitte mithilfe von Brennpunktsgleichungen. Er erkennt, dass sich Parabeln als Grenzfälle von Ellipse und Hyperbel auffassen lassen.

1611 muss Kepler erneut aus religiösen Gründen umziehen: Von Linz aus kartographiert er Oberösterreich, verfasst ein Buch über die Geometrie der Optik (Dioptrice) und erklärt darin, wie der Strahlengang in optischen Geräten verläuft. Außerdem entwirft er ein neues Fernrohr, bei dem er sowohl für das Okular als auch für das Objektiv eine Sammellinse verwendet (im Unterschied zum galileischen Fernrohr von 1610, bei dem das Okular eine Zerstreuungslinse ist). 1613 heiratet er Susanne Reuttinger; von sechs Kindern überlebt nur eines. Als seine Mutter wegen Hexerei angeklagt wird, kümmert er sich um deren Verteidigung; sie kommt zwar nach fünfjähriger Haft frei, stirbt aber an den Folgen der Folterungen.

Kepler hat bereits im Jahr 1601 im Auftrag des Kaisers Rudolph II. (und in Nachfolge Brahes) damit begonnen, ein umfassendes astronomisches Tafelwerk zu erstellen, aus dem man zu jedem Zeitpunkt die Position der Sonne, des Mondes, der Planeten sowie die von über 1000 Sternen ablesen kann (außerdem die Zeitpunkte der Sonnen- und Mondfinsternisse). Als dann John Napier 1614 die Logarithmen erfindet, erkennt er sofort, dass hiermit die aufwendigen Berechnungen beschleunigt werden können; er verfasst eine Anleitung zum logarithmischen Rechnen, die wesentlich zur Verbreitung dieser Rechenmethode beiträgt. Die 1627 erscheinenden »rudolphinischen Tafeln« bleiben über 200 Jahre wichtige Grundlage für Berechnungen in der Astronomie.

1626 muss er – da er nicht zum katholischen Glauben übertreten will – auch aus Linz wegziehen. Er nimmt eine Stelle als Mathematiker bei Fürst Wallenstein an, dem berühmten Feldherrn des 30-jährigen Krieges. Als Wallenstein seinen Posten als Generalissimus des Kaisers verliert, muss sich Kepler erneut auf Reisen begeben. Er versucht, ausstehende Honorare einzutreiben; während eines Aufenthalts in Regensburg erkrankt er und stirbt. Sein Grab wird in den Kriegswirren des 30-jährigen Krieges zerstört.

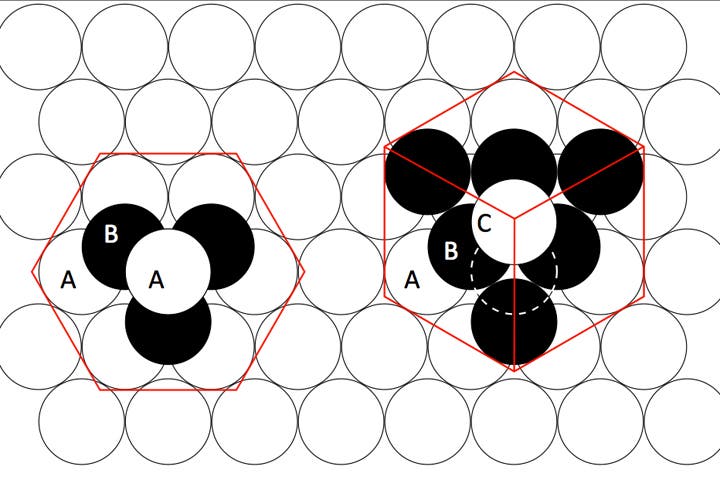
Keplers Beiträge zur Mathematik beschränken sich nicht nur auf die neuartige Behandlung der Kegelschnitte und die logarithmischen Rechnungen. Er entdeckt die sechszählige Symmetrie der Schneekristalle. Auch untersucht er die Frage, wie man Kugeln stapeln muss, damit sie möglichst dicht liegen. Kepler vermutet: Man legt die erste Schicht Kugeln so wie abgebildet aneinander; bei der nächsten Lage werden die Kugeln in die entstandenen Vertiefungen gelegt – dabei bleibt jede zweite Vertiefung leer. Dass diese so genannte Hexagonalpackung tatsächlich die dichteste Kugelpackung darstellt, kann Jahrhunderte lang nicht bewiesen werden; erst die Herleitungen des Amerikaners Thomas Hales aus dem Jahr 1998 haben die Keplersche Vermutung endgültig beweisen. Außerdem beschäftigt sich Kepler systematisch mit Polyedern und klassifiziert sie. Er entdeckt dabei zwei Sternkörper, die dadurch entstehen, dass fünfseitige Pyramiden auf ein Dodekaeder beziehungsweise dreiseitige auf ein Ikosaeder aufgesetzt werden; deren Spitzen selbst bilden umgekehrt ein Ikosaeder beziehungsweise ein Dodekaeder.

Kepler entwickelt auch ein Verfahren zur näherungsweisen Bestimmung des Volumens von Fässern und von vielen anderen Rotationskörpern (»Nova stereometria doliorum vinariorum« – Neue Stereometrie der Weinfässer); bei seiner Herleitung knüpft er an die Methode des Archimedes an, der bereits in der Lage war, Flächen-Maßzahlen bei Parabeln zu bestimmen. Anlass für seine umfangreichen Untersuchungen ist eine ärgerliche Beobachtung beim Einkauf von Weinfässern für seine (zweite) Hochzeitsfeier: Die Weinhändler bestimmen den Inhalt der Fässer dadurch, dass sie einen Stab durch das Spundloch einführen und die Länge \(x\) bis zu den Rändern der Böden messen und dann hiermit das Volumen mithilfe der Formel \(V \approx 0,6 \cdot x^3 \) berechnen – egal, welche Form die Fässer haben.

Die heute unter dem Namen keplersche Fassregel bekannte Formel gibt allerdings nicht das Volumen des Rotationskörpers an, sondern den Flächeninhalt eines durch den Graphen einer Funktion \(f\) begrenzten Flächenstücks auf dem Intervall \([a, b]\), dessen Form durch einen Parabelbogen approximiert wird:

\[\int_a^b f(x)\ dx \approx \frac {b-a}{6} \cdot \left[f(a)+4\cdot f \left( \frac{a+b}{2}\right) + f(b) \right]=\frac{1}{3}(2S+T)\]

Dabei ist \(S\) der Flächeninhalt der beiden Sehnenvierecke und \(T\) der des Tangentenvierecks. (Ist \(f\) eine quadratische Funktion, dann gilt sogar die Gleichheit.) Hieraus ergibt sich folgende Näherungsformel für das Volumen:

\[ V\approx \pi \cdot \frac{b-a}{6} \cdot \left[f^2(a) +4 \cdot f^2 \left(\frac{a+b}{2}\right) + f^2(b)\right] \]

Und im symmetrischen Fall eines Fasses ergibt sich mit den am Boden beziehungsweise in der Mitte des Fasses gemessenen Radien\(r=f(a)=f(b)\) und \(R=f\left(\frac{a+b}{2}\right)\) bezieungsweise den zugehörigen Kreisumfängen \(u\) beziehungsweise \(U\) sowie der Fasshöhe \(h\) die Näherungsformel: